Классификация экспертных оценок диагностики дефектов, определяющих работоспособность портовых кранов c применением ТГМ

В теории грубых множеств (ТГМ) задача классификации формируется следующим образом [42]. Имеется заданное множество примеров, в качестве которых могут выступать, например, множества экспертных оценок различного рода объектов, явлений, событий и др.

Такое исходное множество называют обучающим множеством или обучающим универсумом. Априори известна принадлежность каждого примера к некоторому классу из заданного множества классов, и каждый пример характеризуется набором значений классификационных признаков (атрибутов). С учетом этого, ТГМ позволяет выполнить моделирование зависимостей «значения классификационных атрибутов примера - принадлежность примера определенному классу» [42]. Введено понятие качества обучения (q), которое обозначает относительное количество корректно классификационных примеров:

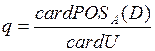(4.29)

где card - означает кардинальное число (мощность) множества А; А ={a, b, c,...} – множество классификационных атрибутов; D = {d} – атрибут (переменная) класса; U – обучающий универсум; POS – положительная область А.

Рассмотрим задачу классификации экспертных оценок основных дефектов, определяющих работоспособность портовых портальных кранов.

Введем следующие классификационные атрибуты показателей дефектов: k₁ – нарушение лакокрасочного покрытия и коррозия несущих элементов; k₂ – трещины, разрывы в швах, околошовной зоне, зонах, удалённых от швов; k₃ – разрывы, срез не менее 10% болтов в соединениях, где болты работают, на растяжение, на срез; k₄ – деформация элементов ферменных, листовых конструкций; k₅ – расслоение металла; k₆ – любые дефекты, возникшие в местах предыдущего ремонта, не попадающие под вышеприведённые определения.

Обозначим через H атрибут, характеризующий классы интегрированного показателя качества программных средств со следующими градациями оценок: „0” – высокая степень риска; „1” – низкая степень риска. Через X = {х₁,х₂,...,х_i...,х_п} обозначим состав экспертной группы. С учетом сказанного, представим исходный обучающий универсум в виде таблицы 4.20. Положим п = 10.

Таблица 4.20