Объединение нечетких отношений

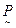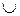
Пусть и – два нечетких отношения. Значения функции принадлежности их объединения 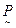определяют по выражению:

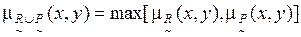. (4.3)

Рассмотрим пример из [42]. В таблицах 4.4 и 4.5 представлены значения двух нечетких отношений и .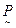

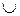
Необходимо определить их объединение 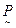(табл. 4.6):

Таблица 4.4	Таблица 4.5	Таблица 4.6
Нечеткое отношение	Нечеткое отношение	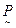Объединение и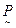

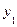
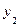
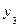
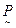
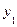
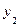
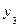
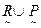
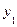
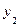
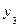
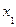
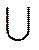
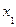
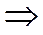
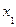
	0,3	0,2	0,1			0,2	0,2	0,2			0,3	0,2	0,2
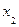
	0,4		0,5		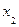0,5	0,2		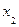	0,5	0,2
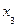
		0,3	0,2		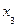	0,6	0,6	0,1		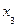		0,6	0,2

Пересечение нечетких отношений

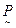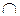
Пусть и – два нечетких отношения. Значение функции принадлежности их пересечения 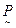определяется так:

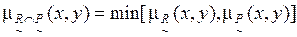. (4.4)

Рассмотрим пример, используя для этого значения таблиц 4.7, 4.8, 4.9:

Таблица 4.7	Таблица 4.8	Таблица 4.9
Нечеткое отношение	Нечеткое отношение	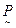Пересечение и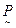

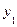
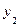
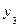
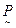
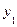
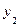
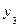
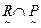
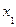
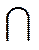
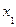
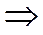
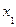
	0,3	0,2	0,1			0,2	0,2	0,2			0,3	0,2	0,1
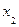
	0,4		0,5		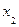0,5	0,2		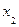	0,4		0,5
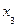
		0,3	0,2		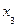	0,6	0,6	0,1		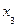	0,6	0,3	0,1

Дополнение нечеткого отношения

Дополнением нечеткого отношения является нечеткое отношение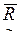

со значениями функции принадлежности:

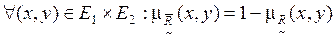. (4.5)

Рассмотрим пример:

Таблица 4.10	Таблица 4.11
Нечеткое отношение	Дополнение нечеткого отношения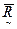

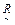
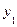
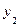
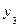
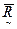
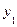
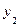
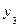
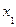
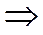
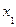
	0,2	0,3	0,4			0,8	0,7	0,6
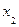
		0,6		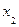		0,4
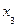
	0,4	0,5	0,3			0,6	0,5	0,7