Исходные данные, характеризующие элементы заданного универсума U
| Элементы (эксперты) | Значения признаков | ||
| а1 | а2 | а3 | |
| х1 | |||
| х2 | |||
| х3 | |||
| х4 |
Продолжение таблицы 4.19
| Элементы (эксперты) | Значения признаков | ||
| а1 | а2 | а3 | |
| х5 | |||
| х6 | |||
| х7 | |||
| х8 | |||
| х9 | |||
| х10 |
Сформируем разделение элементов U на элементарные и обобщенные категории, используя отношения эквивалентности R1, R2, R3 по каждому из признаков а1, а2, а3. Имеем:
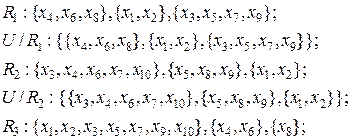 (4.24)
(4.24)
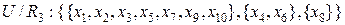 .
.
Сформируем некоторые основные категории на основе комбинаций пересечений отношений эквивалентности R1, R2, R3 по различным значениям признаков a1, а2, а3:
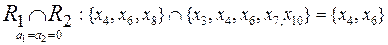 ;
;
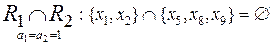 ;
;
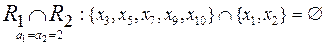 ;
;
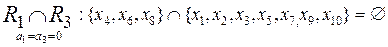 ;
;
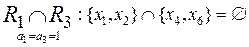 ;
;
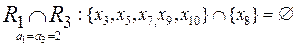 ;
;
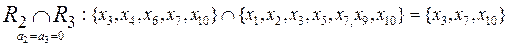 ; (4.25)
; (4.25)
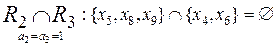 ;
;
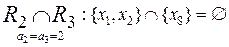 ;
;
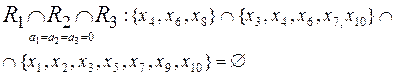 ;
;
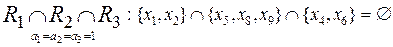 ;
;
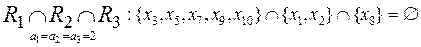 .
.
Приведенные выражения свидетельствуют о том, что основные категории на универсуме U существуют только при пересечениях R1 Ç R2 (a1 = a2 = 0) и R2 Ç R3 (a2 = a3 = 0).
Сформируем более сложные основные категории с использованием пересечений и объединений эквивалентности R1, R2, R3:
Например:
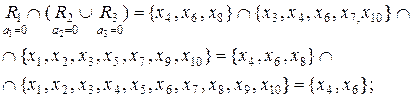
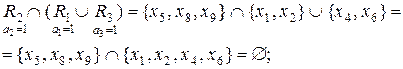 (4.26)
(4.26)
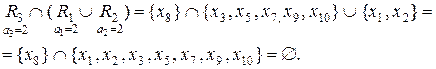
Таким образом, формирование различных категорий на определенном универсуме U позволяет получить семейство отношений эквивалентности, которое будет определять базу знаний на U.
Обратимся опять к таблице 4.19 и выделим классы эквивалентности Е (основные категории), основываясь на значениях всех трех классификационных признаков:
E1={x1, x2}; E2={x3, x7, x10}; E3={x4, x6}; E4={x5, x9}; E5={x8}.
Пусть в результате повторной экспертизы сформировались два класса экспертов, представленных целевыми подмножествами Х1 = {х1, х2, х8}, Х1Í U и X2={x1, x2, x3, x7}, X2ÍU, которые нужно проверить на R-определимость (R-неопределимость).
Первое множество Х1 может быть однозначно представлено как объединение основных категорий Е1 и Е5, т.е. Х1 = Е1 È Е5 = {х1, х2} È {х8} = {х1,х2,х8}. Поэтому Х1 является R-определенным или R-точным.
Множество Х2 включает в себя основную категорию Е1 и два элемента из категорий Е2: х3 и х7, но не всю эту категорию. Поэтому Х2 считается R-неопределенным или R-грубым.
Представим целевые множества Х1 и Х2 в следующем виде:
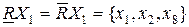 ;
;
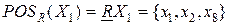 ;
;
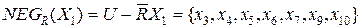 ;
;
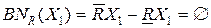 ;
;
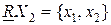 ; (4.27)
; (4.27)
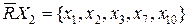 ;
;
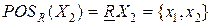 ;
;
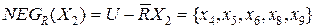 ;
;
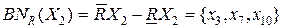 .
.
Для рассматриваемых целевых множеств X1 = {х1, х2, х8} и X2 ={х1, х2, x3, х8} подсчитаем оценки (4.22) и (4.23):
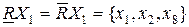 ;
; 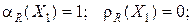
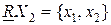 ;
; 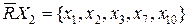 ; (4.28)
; (4.28)
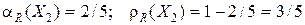 .
.
Дата добавления: 2021-03-18; просмотров: 473;











