Проверка нечетких бинарных отношений на транзитивность в задачах экспертного упорядочения альтернатив

Одной из типовых задач принятия решений является определение порядка (строгого или нестрогого) на множестве альтернатив, что означает оценивание относительной важности каждой из них. При этом важным условие решения такой задачи является проверка полученных упорядочений на транзитивность, которое называют основным правилом логического вывода. 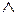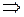Напомним, что отношение R на множестве X называется транзитивным, если для любых элементов x_i, x_j, x_k Î X, x_iRx_j x_jRx_k x_iRx_k. Примерами транзитивных отношения являются отношения «x_i больше x_j» или «x_i меньше x_j». Отношение R на множестве X является отношением строгого порядка, если оно транзитивно и антисимметрично (т.е. ни для каких элементов x_i, x_j Î X не может быть, что x_iRx_j и x_jRx_i). С помощью этого отношения элементы множества X могут быть упорядочены по некоторому заданному признаку. Отношение R на множестве X является отношением нестрогого порядка, если оно транзитивно, антисимметрично и рефлексивно (т.е. для любого x_i Î X, x_iRx_i).

Соответственно выражению (4.8) проверка заданного нечеткого бинарного отношения на транзитивность заключается в следующем [42]. Прежде всего, необходимо задать , например, в виде таблицы, отображающей в числовом виде степени принадлежности пар (x_i, y_j) данному нечеткому отношению (табл. 4.18), и по этим значениям построить нечеткий граф (рис.4.1)

Таблица 4.18

Табличная форма представления

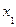
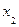
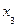
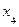
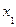
		0,8
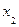
	0,2
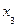
	0,3	0,4		0,1

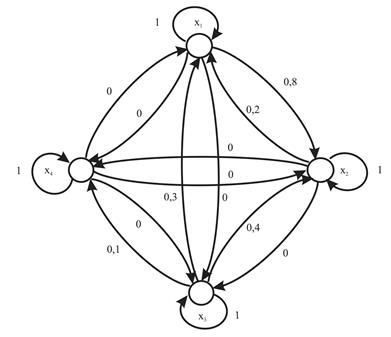
Рис. 4.1. Нечеткий граф, отображающий, заданное

Далее, для каждой вершины графа необходимо сравнить значение функций принадлежности 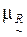для дуги, выходящей из этой вершины и входящей обратно в вершину, со значениями функции принадлежности для каждого набора дуг, по которым можно выйти и снова достичь рассматриваемой вершины. Аналогично, значения функции принадлежности для каждой дуги, соединяющей две вершины графа, необходимо выполнить сравнение со значениями функции принадлежности для всех возможных наборов дуг, соединяющих рассматриваемую пару вершин нечеткого графа.

Сравнение значений функции принадлежности проводится по условию (4.8). Предварительно, исходя из табл. 4.18, можно установить, что заданное рефлексивно (на главной диагонали матрицы располагаются только единицы) и антисимметрично, что легко проверяется путем сравнения значений 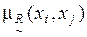, , 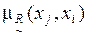i,j=1,2,3,4.

Выполним необходимые расчеты по определению транзитивности или нетранзитивности заданного .

1) Для дуги (x₁, x₁) имеем:

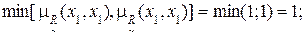
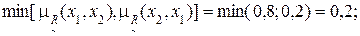
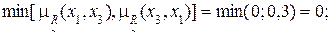
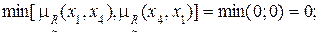
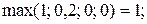
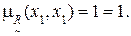
2) Для дуги (x₁, x₂) имеем:

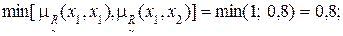
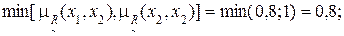
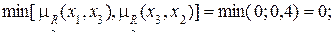
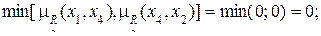
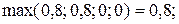
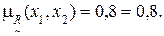
3) Дуга (x₁, x₃):

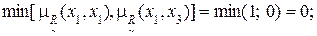
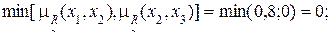
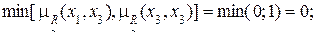
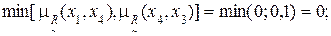
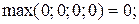
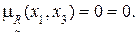
4) Дуга (x₁, x₄):

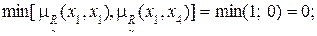
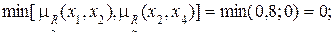
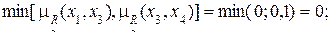
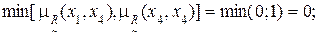
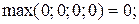
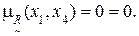
Аналогичные действия выполняются для других дуг графа (рис. 4.1).

5) Дуга (x₂, x₁).

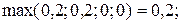
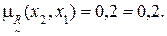
6) Дуга (x₂, x₂).

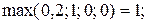
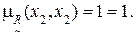
7) Дуга (x₂, x₃).

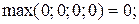
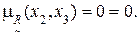
8) Дуга (x₂, x₄).

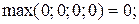
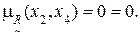
9) Дуга (x₃, x₁).

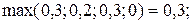
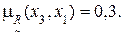
10) Дуга (x₃, x₂).

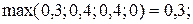
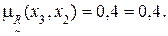
11) Дуга (x₃, x₃).

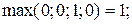
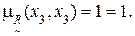
12) Дуга (x₃, x₄).

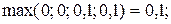
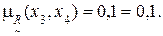
13) Дуга (x₄, x₁).

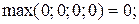
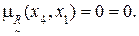
14) Дуга (x₄, x₂).

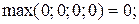
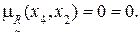
15) Дуга (x₄, x₃).

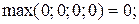
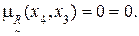
16) Дуга (x₄, x₄).

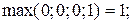
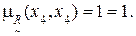
На основании выполненных расчетов можно сделать заключение, что по всем анализируемым дугам выполняется условие (4.8), т.е. нечеткое бинарное отношение является транзитивным.