Качественный анализ организационных структур судостроительных и судоремонтных предприятий с применением комбинированного метода МАИ–ТДШ
В современных условиях, когда отечественное судостроение практически лишено инвестиционных вложений и не имеет возможности модернизироваться, одним из путей повышения эффективности существующего производства может быть проведение анализа с целью выявления тех факторов, которые оказывают влияние на себестоимость постройки судов (накладные расходы, стоимость материалов, расходы на содержание и эксплуатацию оборудования и др.). К числу таких факторов может быть отнесена задача оптимизации организационных структур управления предприятиями.
Одним из ключевых факторов эффективности организационной структуры (системы) является оптимальность иерархии управления. Выбор оптимальной иерархии проводится в соответствии с некоторыми критериями, важнейшими из которых являются: Q1 – норма управляемости, и Q2 – затраты на содержание структуры. Первый критерий характеризует распределение обязанностей и подчиненность между исполнителями структуры, квалификацию менеджеров и др. Второй – несет в себе информацию о затратах на оплату труда, аренду зданий и помещений, коммунальных услуг и др. Норма управляемости r характеризует максимальное количество непосредственных подчиненных, которыми управляет один менеджер в пределах 1≤r≤n (n – число элементов структуры) [1]. Таким крайним значениям r соответствуют графы типа «цепочка» и «веер» (рис. 3.12а, в).
Для поиска оптимальных иерархических структур по двум указанным критериям необходимо последовательно сформировать некоторое множество промежуточных структур, лежащих в интервале между крайними значениями нормы управляемости и решить задачу двухкритериального их ранжирования. Формирование различных организационных иерархических структур может быть проведено в режиме имитационного моделирования с применением теории графодинамических систем [1, 2], в основе которой лежит комплекс операций, позволяющих получать последовательность, сменяющих один другого, иерархических графов с различными показателями Q1 и Q2 (рис. 3.11).
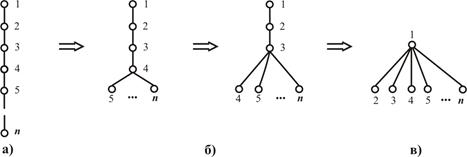
Рис. 3.12. Графическое представление графодинамического моделирования норм управляемости иерархическими структурами:
а) граф-цепочка (r=min); б) промежуточные иерархии;
в) граф-веер (r=max)
При этом число сгенерированных таким образом структур m может быть достаточно большим, например m>10, что может создать сложности при их последующем анализе с использованием классического метода анализа иерархий (МАИ) [33, 35]. Это связано с необходимостью построения большого числа матриц попарных сравнений на согласованность локальных приоритетов, которая при большем числе сравниваемых элементов, как правило, не выполняется. В данной ситуации для решения задачи ранжирования альтернативных иерархических структур целесообразно использовать подход, объединяющий в себе возможности МАИ и теории свидетельств Демпстера-Шейфера (ТДШ).
Рассмотримподход к ранжированию множества альтернативных иерархических структур, характеризующихся различными значениями критериев Q1 и Q2 с использованием метода МАИ/ТДШ. В данном подходе, вместо сравнения отдельных альтернатив между собой, эксперту или лицу, принимающему решение (ЛПР), предлагается по каждому из критериев выделить из исходного множества всех альтернатив ряд подмножеств, а затем определить степени их предпочтения по отношению ко всем оставшимся альтернативам, что эквивалентно заданию парного сравнения таких подгрупп и всего множества альтернатив.
Далее обработка результатов экспертного опроса и вычисление весов альтернатив осуществляется с использованием ТДШ. При этом в соответствии с правилом комбинирования свидетельств Демпстера вычисляются комбинированные базовые вероятности и определяются функции доверия и правдоподобия для всех подгрупп альтернатив, включая подмножества, состоящие из одной альтернативы. На основании значений этих функций принимается решение о выборе той или иной альтернативы.
Рассмотрим пример применения описанного подхода, сопровождая его числовыми значениями. Пусть на множестве альтернатив 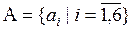 по каждому из критериев сформированы следующие подмножества:
по каждому из критериев сформированы следующие подмножества:
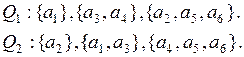 (3.22)
(3.22)
Предварительно, как делается в МАИ, определяются веса w критериев Q1 и Q2 посредством их парного сравнения. Положим, что w(Q1)=0.6 и w(Q2)=0.4. Далее оцениваются степени предпочтения выбранных подмножеств (1) с использованием шкалы, имеющей шесть значений от 1 до 6 (1 – означает эквивалентность альтернатив или невозможность их сравнения, а значение 6 означает абсолютную степень превосходства).
Результаты такого оценивания по критериям Q1 и Q2 представлены в таблицах 3.28 и 3.29.
Таблица 3.28
Результаты сравнения альтернатив по критерию Q1
| w(Q1)=0,6 | {a1} | {a3 ,a4} | {a2 ,a5 ,a6} | {a1 ,a2 ,a3 ,a4 ,a5 ,a6} |
| {a1} | 2 × (0,6) | |||
| {a3 ,a4} | 4 × (0,6) | |||
| {a2 ,a5 ,a6} | 6 × (0,6) | |||
| {a1 ,a2 ,a3 ,a4 ,a5 ,a6} | 1/(2×0,6) | 1/(4×0,6) | 1/(6×0,6) |
Таблица 3.29
Результаты сравнения альтернатив по критерию Q2
| w(Q2)=0,4 | {a2} | {a1 ,a3} | {a4 ,a5,a6} | {a1 ,a2 ,a3 ,a4 ,a5 ,a6} |
| {a2} | 3 × (0,4) | |||
| {a1 ,a3} | 4 × (0,4) | |||
| {a4 ,a5,a6} | 5 × (0,4) | |||
| {a1 ,a2 ,a3 ,a4 ,a5,a6} | 1/(3×0,4) | 1/(4×0,4) | 1/(5×0,4) |
Таблица 3.30
Результаты сравнения альтернатив по критериям Q1 и Q2
| Q2 | Q1 | |||
| {a1} | {a3 ,a4} | {a2 ,a5 ,a6} | {a1 ,a2 ,a3 ,a4 ,a5 ,a6} | |
| {a2} | Ø | Ø | {a2} | {a2} |
| {a1 ,a3} | {a1} | {a3} | Ø | {a1 ,a3} |
| {a4 ,a5,a6} | Ø | {a4} | {a5 ,a6} | {a4 ,a5 ,a6} |
| {a1 ,a2 ,a3 ,a4,a5 ,a6} | {a1} | {a3 ,a4} | {a2 ,a5 ,a6} | {a1 ,a2 ,a3 ,a4 ,a5 ,a6} |
Далее выполняются преобразования значений предпочтений полученных матриц посредством умножения и деления их значений, исходя из следующего правила: каждое значение предпочтения xij, назначенное по указанной шкале, т.е. xij Î[1, 6] и находящееся на пересечении i-ой строки и j-го столбца равно w×xij, если xij ≥ 1 и 1/(w× xij), если xij<1.
Посчитаем веса подмножеств альтернатив (3.22) по критериям Q1 и Q2 в виде собственных значений. Нулевые элементы парных сравнений в вычислениях не используются.
Веса альтернатив по критерию Q1:
Веса выделенных подмножеств исходного множества альтернатив А, по каждому из критериев, вычисляются по формуле (3.16).
Рассчитаем веса выделенных подмножеств альтернатив:
-по критерию Q1:
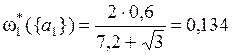 ;
; 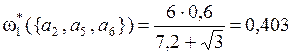 ;
;
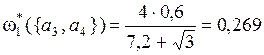 ;
;
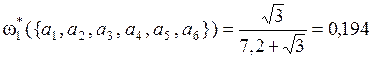 .
.
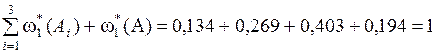 .
.
– по критерию Q2:
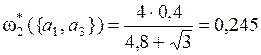 ;
; 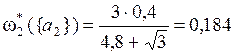 ;
;
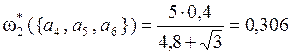 ;
;
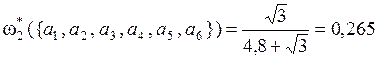 .
.
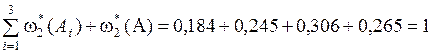 .
.
Коэффициент конфликтности(3.6):
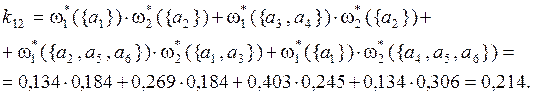
Рассчитаем комбинированные массы вероятности выделенных подмножеств альтернатив по критериям Q1 и Q2 на основе правила Демпстера:
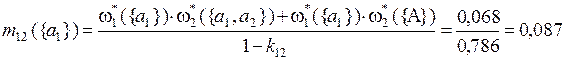 ;
;
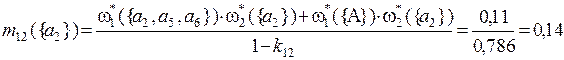 ;
;
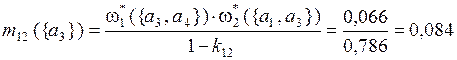 ;
;
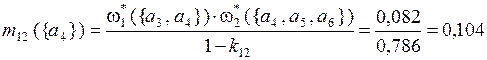 ;
;
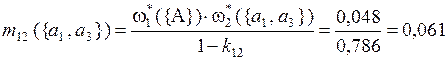 ;
;
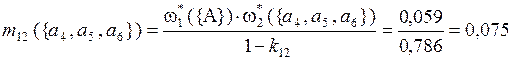 ;
;
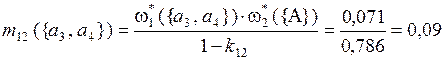 ;
;
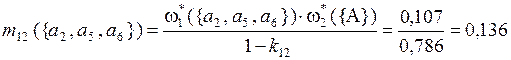 ;
;
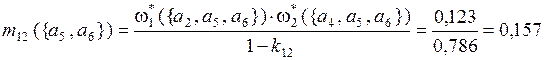 ;
;
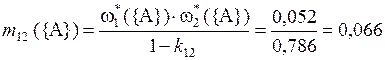 ;
;
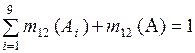 .
.
По комбинированным массам вероятностей m12(Ai) вычислим значения функции доверия Bel({Ai}) и правдоподобия Pl({Ai}) для каждой исходной альтернативы:
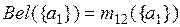 =0,087;
=0,087;
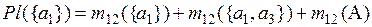 =0,087+0,066=0,214;
=0,087+0,066=0,214;
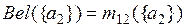 =0,14;
=0,14;
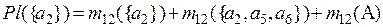 =0,14+0,136+0,066=0,342;
=0,14+0,136+0,066=0,342;
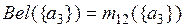 =0,084;
=0,084;
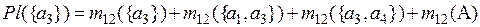 =0,084+0,087+
=0,084+0,087+
+0,09+0,066=0,301;
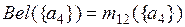 =0,104;
=0,104;
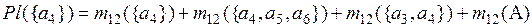 =
=
=0,104+0,075+0,09+0,066=0,335;
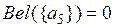 ;
;
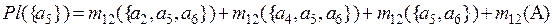 =0,136+
=0,136+
+0,07+5+0,157+0,066=0,434;
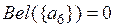 ;
;
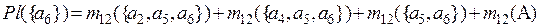 =0,434.
=0,434.
Для определения степени превосходства исходных альтернатив воспользуемся коэффициентом пессимизма γÎ[0,1] и рассчитаем результирующие значения:
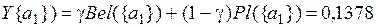 ;
; 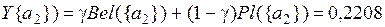 ;
;
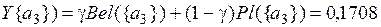
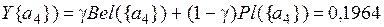 ;
;
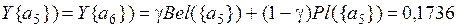 .
.
Из полученных результатов видно, что наибольшее значение функций Bel и Pl имеет вторая альтернатива, следовательно, она является оптимальной (наиболее приемлемой) по выбранным критериям Q1 и Q2 .
При этом, итоговая ранжировка альтернативных иерархических структур имеет вид:
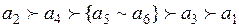 . (3.23)
. (3.23)
Основным достоинством рассмотренного подхода по сравнению с классическими МАИ является то, что в нем отсутствует несогласованность матриц попарных сравнений групп альтернатив. Это связано с тем, что выбранные экспертом или ЛПР группы альтернатив, соответствующие одному критерию, не пересекаются.
Метод МАИ/ТДШ целесообразно применять, когда отсутствует информация о предпочтительности каждой отдельной альтернативы по тому или иному критерию. Вместе с тем, данный метод требует более тщательного подхода к подбору экспертов, которые должны быть высокопрофессиональными специалистами в конкретных предметных областях, и обладать способностями выделять и оценивать только те группы альтернатив, по которым они могут определить предпочтения по отношению к другим альтернативам.
Глава 4.
Дата добавления: 2021-03-18; просмотров: 510;











