Базовые логические элементы
Для физической реализации логической функции в технике используется электронная схема (цифровое устройство), выполняющая соответствующее этой функции преобразование информации (то есть, логические операции над двоичными переменными). Для реализации элементарных логических функций используют логические элементы.
Логическим элементом называется физическое устройство, реализующее одну из операций алгебры логики или простейшую логическую функцию. Схема, составленная из конечного числа логических элементов, называется логической схемой.
Число входов логического элемента соответствует числу аргументов воспроизводимых им одной или нескольких булевых функций.
Подобно тому, как сложная булева функция может быть получена суперпозицией более простых функций, так и сложное цифровое устройство строится из элементарных схем, в частности, из логических элементов.
Набор логических элементов называется функционально полным, если реализуемые этими элементами логические функции образуют функционально полную систему логических функций. Так функционально полным является набор, состоящий из трех логических элементов – инвертора, конъюнктора и дизъюнктора. Условные графические обозначения и таблицы истинности этих элементов показаны, соответственно, на рисунках 5.9, 5.10 и 5.11.
| № | х | у = 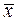
|

Рисунок 5.9 – УГО и таблица истинности инвертора
| № | х2 | х1 | у = х1 + х2 |
 0 0
| |||
Рисунок 5.10 – УГО и таблица истинности дизъюнктора
 № №
| х2 | х1 | у = х1×х2 |
Рисунок 5.11 – УГО и таблица истинности конъюнктора
Интерпретацией логического элемента ИЛИ (дизъюнктора) может служить схема, изображенная на рисунке 5.12. Действительно, свечение лампы накаливания Н возможно, если замкнут ключ S1, или ключ S2, или замкнуты оба ключа (другими словами – если замкнут хотя бы один ключ S, то есть, если хотя бы одна переменная Si равна логической 1).
 |
Рисунок 5.12 – Иллюстрация функционирования дизъюнктора
Аналогично функционирование логического элемента И (конъюнктора) можно проиллюстрировать схемой, приведенной на рисунке 5.13.
Свечение лампы накаливания Н в схеме на рисунке 5.13 возможно только тогда, когда замкнут и ключ S1 и ключ S2(то есть только тогда, когда обе переменные Si равны логической 1). То есть, функционирование схемы можно описать таблицей истинности, приведенной на рисунке 5.11 для конъюнктора.

Рисунок 5.13 – Иллюстрация функционирования конъюнктора
Как отмечалось ранее, функциональной полнотой обладают логические функции отрицание конъюнкции (И-НЕ) и отрицание дизъюнкции (ИЛИ-НЕ), для реализации которых используются соответствующие логические элементы Шеффера (И-НЕ) и Пирса (ИЛИ-НЕ), каждый из которых представляет собой функционально полный набор логических функций. Условные графические обозначения и таблицы истинности этих элементов приведены, соответственно, на рисунках 5.14 и 5.15.
| № | х2 | х1 | 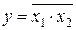
|
 0 0
| |||
Рисунок 5.14 – УГО и таблица истинности логического элемента И-НЕ
| № | х2 | х1 | 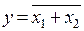
|

Рисунок 5.15 – УГО и таблица истинности логического элемента ИЛИ-НЕ
Покажем, что элемент Шеффера обладает функциональной полнотой, то есть, что с его помощью можно реализовать логические функции И, ИЛИ и НЕ.
Из таблицы истинности (рисунок 5.14) видно, что при выполнении условия х1 = х2 функция у равна инверсному значению входных логических переменных. Следовательно, объединив входы элемента, как показано на рисунке 5.16, получим инвертор.

Рисунок 5.16 – Инвертор на основе элемента 2И-НЕ
Если к функции 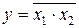 применить инверсию, то на основе теоремы о двойном отрицании получим
применить инверсию, то на основе теоремы о двойном отрицании получим
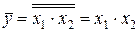 . (5.5)
. (5.5)
Из (5.5) видно, что конъюнкцию логических переменных можно получить, включив после элемента Шеффера еще один такой же элемент, реализующий функцию НЕ (рисунок 5.17).
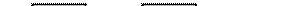
Рисунок 5.17 – Конъюнктор на основе элементов 2И-НЕ
И, наконец, воспользовавшись правилом де Моргана, получим
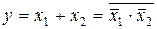 . (5.6)
. (5.6)
Выражение (5.6) описывает схему включения элементов Шеффера для реализации дизъюнкции логических переменных (рисунок 5.18).
 |
Рисунок 5.18 – Дизъюнктор на основе элементов 2И-НЕ
Аналогично можно показать, что элемент Пирса (ИЛИ-НЕ) также обладает функциональной полнотой.
Системой логических элементов называется предназначенный для построения цифровых устройств функционально полный набор логических элементов, объединяемый общими электрическими, конструктивными и технологическими параметрами, использующий одинаковый способ представления информации и одинаковый тип межэлементных связей. Система элементов чаще всего избыточна по своему функциональному составу, что позволяет строить схемы, более экономные по числу использованных элементов. Системы элементов содержат элементы для выполнения логических операций, запоминающие элементы, элементы, реализующие функции узлов ЭВМ, а также элементы для усиления, восстановления и формирования сигналов стандартной формы.
Элементы, входящие в состав системы, представляют собой микроминиатюризованные интегральные электронные схемы (микросхемы), сформированные в кристалле кремния с помощью специальных технологических процессов.
В большинстве современных систем (серий) элементов имеются микросхемы малой степени интеграции (ИС), средней степени интеграции (СИС) и большой степени интеграции (БИС). Логические элементы в виде схем ИС реализуют совокупность логических операций, таких, как И, ИЛИ, И-ИЛИ, И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ и триггеры. Логические элементы на микросхемах СИС и БИС реализуют узлы ЭВМ.
Основными параметрами системы логических элементов являются:
- уровни питающих напряжений;
- уровни сигналов для представления логических 0 и 1;
- нагрузочная способность (коэффициент разветвления по выходу);
- помехоустойчивость;
- рассеиваемая мощность;
- быстродействие.
По типам базовых элементов электронных ключей разделяют несколько типов интегральных элементов, где наиболее распространенными являются следующие:
а) транзисторно-транзисторная логика (ТТЛ);
б) эмиттерно-связанная логика (ЭСЛ);
в) инжекционная интегральная логика (И2Л);
г) структуры металл-оксид-полупроводник р-типа (р-МОП);
д) структуры металл-оксид-полупроводник п-типа (п-МОП);
е) комплементарные МОП-структуры (КМОП);
ж) динамические МОП-структуры.
Логические схемы, которые изготовляются на разной конструктивно-технологической основе, значительно различаются по своим характеристикам, даже если они реализуют одинаковые функции. У любого из указанных видов схемотехники имеются свои преимущества и недостатки. Так, ЭСЛ отличается высоким быстродействием, хотя некоторые разновидности ТТЛ приближаются к ней по этому параметру. Как р-МОП-, так и п-МОП-логика широко применяются в микропроцессорах, а КМОП-схемотехника пользуется преимуществом, если важно уменьшить потребляемую мощность.
Динамические МОП-структуры используются для построения различных запоминающих устройств. Они имеют простую организацию, в которой логическое состояние определяется зарядом емкости, внутренне присущей логическому элементу.
Основные параметры ИМС ТТЛ, ЭСЛ и КМОП приведены, соответственно, в таблицах 5.2, 5.3 и 5.4. Проанализировав содержимое таблиц, можно сделать вывод, что наибольшим быстродействием характеризуются ИМС ТТЛ. ИМС КМОП обладают меньшим быстродействием, но у них лучше нагрузочная способность (то есть, к выходу одного элемента можно подключить большее число входов других элементов). В ИМС ЭСЛ наименьшая задержка распространения импульсных сигналов.
Таблица 5.2 – Основные параметры ИМС ТТЛ
| Серия ИМС | Потребляемая мощность, мВт | Задержка распространения, нс | Максимальная частота, МГц | Коэффициент разветвления |
| 10,0 | ||||
| 33,0 | ||||
| 6,0 | ||||
| 9,5 | ||||
| 3,0 | ||||
| КР1533 | 4,0 | |||
| КР1531 | 2,0 |
Таблица 5.3 – Основные параметры ИМС ЭСЛ
| Серия ИМС | Потребляемая мощность, мВт | Задержка распространения, нс | Коэффициент разветвления | Напряжение питания, В |
| 100, 500 | 2,90 | -5,2 | ||
| 0,75 | -4,5 |
Таблица 5.4 – Основные параметры ИМС КМОП
| Серия ИМС | Потребляемая мощность, мВт | Задержка распростран., нс | Максимальная частота, МГц | Коэффициент разветвления | Напряж. питания, В |
| 164, | |||||
| 561, | 3 ... 15 | ||||
| КР1561 | 3 ... 18 | ||||
| 2 ... 6 |
Дата добавления: 2021-11-16; просмотров: 906;











