II. Базовые понятия музыкальной акустики

Рассмотрим теперь современные понятия музыкальной акустики и принципы звукообразования в основных группах музыкальных инструментов.
Источники звука в музыкальных инструментах, которые настраиваются на определенную высоту тем или иным механическим способом, делятся по типу излучателей на несколько групп [6, 7]:
а) источники с колеблющимися струнами;
б) источники с колеблющимися язычками и стержнями;
в) источники с колеблющимися мембранами;
г) источники с колеблющимися пластинами;
д) источники с колеблющимися столбами воздуха (в трубах).

Во многих трудах по акустике констатируется факт распространенности механических колебаний в природе и технике. Утверждается, что колебательные движения и колебательные процессы представляют собой наиболее часто встречающиеся явления нашего мира. Каким образом музыка связана со звуковыми, колебательными движениями? Музыка — искусство, отражающее действительность в звуковых художественных образах. Звук в музыке является носителем художественного образа, и он есть не что иное, как распространяющиеся в упругой воздушной среде механические колебания, воспринимаемые ухом.

Ощущение звука передается нашему уху с помощью механических колебаний частиц воздуха, создающих волны давления и разрежения. Задумаемся о природе этого давления. С очевидностью мы поймем, что в каждой отдельной точке воздушной среды в определенный момент времени это давление будет принимать вполне определенное значение и, следовательно, его можно будет выразить числом. Если же от исполнителей к ушам слушателей будет распространяться информация об игре оркестра в виде волн сжатия и разрежения, то с помощью маленького микрофона, установленного по нашему желанию в подходящем месте зала, мы сможем записать осциллограмму звуковых колебаний в виде кривой, показывающей, как изменяется звуковое давление в выбранной точке во времени.

И вот эта осциллограмма, кривая какой-то сложной формы, будет содержать в себе всю информацию об оркестре, вернее о его звучании: и какие в данный момент времени инструменты играют, и то, что, например, вторая скрипка в первом ряду сыграла одну фальшивую ноту, кашлянул зритель, и т. п. И при этом никакого значения не имеет ни количество музыкантов, ни сложность исполняемой музыки — все это может быть представлено одним единственным графиком, характеризующим изменение звукового давления. Ухо и человеческий мозг на основе этого изменения давления вместе выполняют почти сверхъестественную работу по разгадыванию всей нужной информации и представляют ее нам в простой осознаваемой форме.

Если мы сравним записи звучания двух разных оркестров, например симфонического и джазового, то, к нашему удивлению, нам будет чрезвычайно трудно найти какое-либо характерное различие записанных кривых. Они очень сложны. Мы с гораздо большим успехом сможем заняться изучением сначала простейших колебаний. График простейшего колебания представляет собой синусоиду, которая в свою очередь является «портретом» чистого музыкального тона, который звучит довольно глухо и малоинтересен с музыкальной точки зрения. но имеет ярко выраженную определенность высоты {схема 1). Сравним синусоиду с графиком «белого шума» (схема 2), примером которого является шум аплодисментов или шум морского прибоя и который не имеет какой-либо определенной высоты. Кривая такого графика больше похожа на случайный, хаотичный набор импульсов.

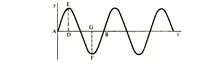
Схема 1. Простое гармоническое колебание. AB – период, DE и GF – амплитуда

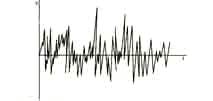
Схема 2. Белый шум

Схемы 1 и 2 представляют два крайних по свойствам звука. Можно сказать, что все другие сложные звуки находятся между этими двумя крайностями: полной регулярности и полной нерегулярности. Начнем с изучения простейших колебаний.

Физическая сущность колебательных процессов, происходящих в вибраторах музыкальных инструментов, различна. Причины колебаний, например, струны, возбужденной ударом, отличаются от причин колебаний язычка в проеме голосовой планки, на который действует поток воздуха, и совсем другая причина колебаний столба воздуха в трубе духового музыкального инструмента. Но даже первое знакомство с законами колебаний вибраторов музыкальных инструментов обнаруживает много одинакового в самих колебательных движениях этих вибраторов.

Благодаря схожести различных колебательных процессов для музыкальных инструментов оказалось возможным выделить два основных типа колебаний:
1) свободные колебания, то есть такие, какие совершает вибратор, первоначально возбужденный и затем предоставленный самому себе. Пример свободных колебаний дает струна фортепиано, ударенная молоточком, деревянная пластинка ксилофона, возбужденная колотушкой и т. д.;
2) вынужденные колебания, то есть такие, какие совершает вибратор музыкального инструмента, на который непрерывно воздействует какая-либо внешняя сила. Если это язычок в аккордеоне или баяне, то внешней силой является поток воздуха; если это струна скрипки, то внешняя сила возникает благодаря трению смычка о струну и т. д.

Укажем на основное различие этих типов колебаний: при свободных колебаниях внешняя возбуждающая сила действует только в первоначальный момент, дальше вибратор колеблется самостоятельно, свободно, на него уже не действует никакая сила (кроме сопротивления воздуха и сил трения в материале вибратора и его опорах). При вынужденных же колебаниях внешняя возбуждающая сила постоянно воздействует на вибратор. В результате такого различия в первом случае колебания относительно быстро прекращаются, во втором — они длятся так долго, как долго существует внешняя сила. Рассмотрим более подробно оба типа колебания.

1. Свободные колебания вибраторов в музыкальных инструментах

Колебательные движения в самом общем виде – это движения туда и сюда, из стороны в сторону. Сравним между собой, например, колебания ветки дерева при порывах ветра разной силы и колебания точки, взятой на середине струны. И ветка дерева и струна совершают движения «из стороны в сторону». Однако оба эти движения принципиально различаются по характеру. Ветка каждый раз может отклоняться на различное расстояние, и ее среднее положение в разные моменты времени будет различным. Точка же на струне всегда совершает движение около положения равновесия, которое она занимает тогда, когда находится в покое. Это первое отличие. Второе отличие более важное. Оно заключается в том, что точка на струне проходит определенное положение (например, положение равновесия) через равные промежутки времени. Движение ветки дерева такого признака не содержит: она проходит какое-либо фиксированное положение через разные промежутки времени. Наконец, есть еще два менее существенных отличия: путь, который проходит ветка, во много раз больше пути, проходимого точкой струны, но зато быстрота движения или иначе – скорость движения у струны гораздо болыие.

Для того чтобы характеризовать оба вида движения, первое обозначают как непериодическое, то есть неповторяющееся строго во времени, а второе – как периодическое, то есть повторяющееся регулярно во времени. Во времени периодически повторяются не только определенные положения точки, но и ее скорости и ускорения. В музыкальной акустике рассматриваются только периодические колебания и такие, периодичность которых нарушается незначительно.

При изучении колебаний обычно не интересуются положением точки в данный момент времени. Например, струна издает звук ля. В какой-то момент времени мы слышим этот звук, но он не определяется положением струны в данный момент времени, а зависит от всего процесса колебаний струны в целом. Установление общих закономерностей всего процесса в целом характерно для рассмотрения различных типов колебаний источников музыкальных звуков.

Посмотрим, каковы колебания точки, находящейся на торце вилки камертона. По движению одной точки еще нельзя судить о движении многих других точек вибратора, и правомерен вопрос: можно ли отождествлять колебания одной точки с колебаниями источника, на котором взята эта точка? Теория колебаний показывает, что такое отождествление хотя и незаконно во всех случаях, но часто весь процесс колебаний может быть представлен так же, как и движение одной единственной точки.

Мы сказали, «посмотрим... колебания точки». Действительно, как сделать видимыми колебания точки на торце вилки камертона? Можно, конечно, мысленно представить себе, что вилки камертона попеременно то сближаются, то удаляются. Обычный камертон стандарта высоты ля¹ не позволит увидеть движение, но если взять большой камертон и прикрепить к одной вилке кусочек грифеля от карандаша, то движение можно сделать видимым. Нужно только быстро и легко провести грифелем на колеблющемся камертоне по полоске бумаги.

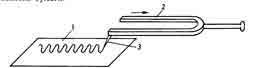
Схема 3. Визуализация колебаний ножек камертона
1 – бумага; 2 – камертон; 3 – карандаш

Таким образом, с помощью большого камертона мы смогли увидеть яснее движение торцов вилок и запечатлеть «портрет» колебания на бумаге. Колебания как бы развернулись во времени; подобный прием изображения колебаний на бумаге так и называется – «разверткой колебаний». Кстати сказать, развертка колебаний может быть осуществлена и другими путями, например, с помощью электронного луча на экране электронно-лучевой трубки.

Камертон можно заставить звучать не только ударом, но и проводя по нему смычком. В этом случае портрет колебаний изобразится плавной кривой – синусоидой. Синусоида – графическое представление какой-либо переменной величины, изменяющейся по закону синуса. В нашем случае так изменяется во времени положение точки на торце вилки камертона.
Многие физические явления в природе происходят в соответствии с законом синуса. Строгая математика считает синусоидальным только такое колебание, которое никогда не начиналось и никогда не кончается. Естественно, что реальные колебательные процессы никогда такому условию не отвечают. Все имеет свое начало и конец. Поэтому принято считать колебания синусоидальными, если они являются таковыми хотя бы на конечном, достаточно длительном отрезке времени.

Важно подчеркнуть, что не сама синусоида представляет интерес, а переносимый ею признак, та информация, которая рассказывает нам о свойствах колебательной системы, о процессах, происходящих с настраиваемыми источниками звука. Человек слышит звук камертона именно потому, что барабанная перепонка в его ухе колеблется в такт с синусоидальными колебаниями камертона.

Выявление общих законов колебаний намного облегчается, если использовать графики колебаний, дающие наглядное представление о характере колебаний. Такой график можно получить либо с помощью прибора, как в вышеприведенном случае, либо вычертить, учитывая закономерности колебаний.

На схеме 3 горизонтальная ось – ось времени, и если провести в какой-то момент времени через эту ось перпендикуляр до пересечения с синусоидой, то точка пересечения покажет, на каком расстоянии находится вилка камертона от центрального положения, то есть положения равновесия.
Говорят, что точка совершает полное колебание, когда она из какого-то фиксированного положения, например из положения покоя, отклоняется в одну сторону, далее опускается до положения равновесия вновь, проходит его, отклоняется в другую сторону и снова возвращается в центральное положение. Время, в течение которого точка, совершающая колебания, проходит все промежуточные положения и возвращается к произвольно выбранному исходному, называется периодом колебаний. Наибольшее отклонение точки от положения равновесия называется амплитудой колебаний. Таким образом, точка совершает одно полное колебание, когда проходит расстояние, равное в сумме четырем амплитудам, а время, затраченное точкой на это движение, равно периоду. Например, период колебания камертона ля¹ равен 0,0022727272 с. Округленно 0,0023 с или 2,3 миллисекунды. Это значительно меньше времени, необходимого глазу для восприятия движения (около 0,1 с), поэтому мы и не в состоянии увидеть колебания ножек камертона ля1.

Число колебаний или число периодов за одну секунду есть частота колебаний. Этот параметр обратно пропорционален периоду, и его можно вычислить, разделив единицу на период. Так частота для колебания с периодом 0,002273 с будет равна 1:0,00273 ≈ 440 колебаний в секунду. Единица частоты – г е р ц. Один герц – одно колебание в секунду, 440 Гц – 440 колебаний в секунду.

Для колебания, представленного на схеме 1, рассмотренные только что параметры – период, частота и амплитуда – постоянные во времени величины. Они постоянны и в первую, и во вторую, и в третью, и в последующие секунды. Но каким же образом постоянные величины могут представлять само движение точки? Мы еще не сказали об одной переменной величине, которая несет непосредственную информацию о движении и зависит от констант (постоянных величин) колебательного процесса. Эта переменная величина – отклонение колеблющейся точки от положения равновесия в данный момент времени. Когда отклонение максимальное, его называют амплитудой, как и было уже установлено выше. Если мы будем знать закон изменения отклонения y во времени, то тем самым будем знать практически все о данном процессе колебания.

Графически закон изменения отклонения во времени уже представлен кривой на схеме, т. е. синусоидой. Поэтому остается только представить эту кривую с помощью соответствующей формулы:

у=А * Sin 2πf * t, (1)

где: А — амплитуда колебания,
f – частота колебания (f = 1/T, где Т — период),
2π – постоянный коэффициент (π = 3,14),
t – текущее время,
у – отклонение колеблющейся точки от положения равновесия в данный момент времени t.

Обозначим произведение постоянного коэффициента 2π на частоту f буквой ω, которую назовем, в отличие от циклической частоты f, круговой частотой: 2πf = ω. Это обозначение будет использовано ниже.

Любое колебательное движение, совершающееся по закону (1), называется гармоническим колебанием. Ему соответствует звук камертона, колебания которого непрерывно поддерживаются смычком. В музыкальной акустике с понятием гармонического колебания связано понятие чистого тона. Именно чистый тон, взаимодействующий с другими чистыми тонами, является «объектом» настройки.

Изменения параметров гармонического колебания вызывают соответствующие изменения тона. Так, увеличение амплитуды вызывает увеличение громкости, а уменьшение или увеличение частоты – понижение или повышение тона. А существует ли связь между амплитудой и частотой? Зависит ли частота от того, насколько сильно возбудили камертон или струну? Ответ – и да, и нет – может показаться на первый взгляд парадоксальным. Из логики ведь известно. что два противоположных суждения об одном и том же предмете не могут быть одновременно истинными, какое-то суждение должно быть ложным. Однако логика такого ответа будет спасена, если учесть, с какой точностью определять изменение частоты при изменении амплитуды.

В первом прнближении можно считать, что параметры не зависят для большинства вибраторов один от другого, если амплитуды колеблющихся струн или язычков достаточно малы. Такое свойство колебаний называется изохронностью, Практически человек не замечает изменения частоты, если первый раз сыграть тон очень тихо (пианиссимо), а второй раз – очень громко (фортиссимо). Да иначе и нельзя было бы играть на инструментах, в которых при изменении громкости изменялась бы частота.

И все же небольшие отклонения от изохронности наблюдаются даже у признанного эталона частоты — камертона: частота очень слабых его колебаний чуть-чуть ниже частоты сильных колебаний. Но ухо таких отклонений частоты попросту не замечает. В данной книге рассматриваются только изохронные колебания или, как их иначе называют, линейные колебания. Если же изохронность нарушается, то колебания называют нелинейными. Большинство вибраторов музыкальных инструментов при очень сильных колебаниях, то есть, больших амплитудах дают нелинейные колебания или, как говорят, становятся нелинейными системами. Но при достаточно малых амплитудах колебания в музыкальных инструментах можно считать линейными.

Мы установили, что гармонические колебания камертона имеют определенную частоту (или обратную ей величину – период) и амплитуду. Допустим, два одинаковых камертона имеют одинаковые амплитуды и частоты. Могут ли чем-то отличаться колебания этих камертонов? Оказывается. могут. Один камертон можно заставить звучать несколько позже, чем другой. Соответствующие графики колебаний будут смещены друг относительно друга (см. схему 4). Такому смещению дали специальное обозначение – с д в и г или, что более употребителыю, разность фаз. Разность фаз определяется расстоянием, отсчитанным по оси времени (горизонтальной оси), однако это смещение по времени удобнее выразить в долях мериода, короче говоря, сопоставить смещение с величиной периода.

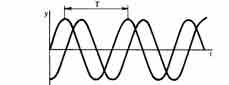
Схема 4. Сдвиг фаз колебаний

Предположим, что в какой-то момент вилки одного камертона отклонились от положения равновесия на максимальную величину, а в тот же самый момент вилки второго камертона проходят положение равновесия. Синусоиды в этом случае сдвинуты на четверть периода (см. схему 4), и колебания различаются по фазе на 90° (полный период принят за 360°).
Для настройки важную роль, как увидим далее, играет разность фаз 0° и разность фаз 180°. Соответствующие пары синусоид показаны на схемах 5 и 6. При нулевой разности фаз графики колебаний

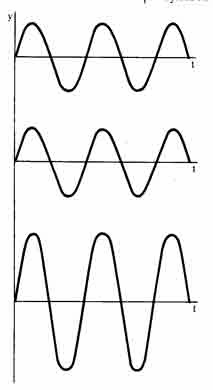
Схема 5. Сложение гармонических колебаний с равными частотами, разность фаз φ = 0^о

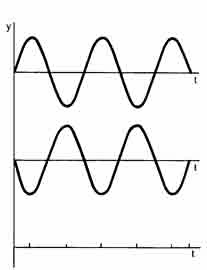
Схема 6. Сложение гармонических колебаний с равными частотами, разность фаз φ = 180^о

камертонов точно совпадают, такие колебания называются с и н ф а з н ы м и. При разности фаз 180° колебания являются как бы зеркальным отражением друг друга. В этом случае вилки одного камертона максимально раздвинуты, а вилки второго камертона максимально сближены в тот же самый момент, в следующий момент положение вилок меняется на противоположное и т. д. Если частоты камертонов в точности совпадают, а разность фаз сохраняется постоянной (и не обязательно равной нулю), то такие колебания называют с и н х р о н н ы м и. Синхронизация колебаний имеет место, например, при настройке унисона. Отметим также, что колебания с разностью фаз 180° называются антифазными, сами колебания происходят в противофазе.

Понятие о разности фаз необходимо при выяснении явлений, происходящих при сопоставлении двух или нескольких гармонических колебаний в процессе настройки вибраторов музыкального инструмента (то есть струн, язычков и т. д.). В этом случае разность фаз сопоставляемых тонов имеет решающее значение.

Сдвиг фаз рассматривался до сих пор как характеристика временного смещения колебаний. Но можно установить понятие фазы и для одного гармо-нического колебания. Тогда фазу, выраженную в долях периода, нужно отсчитывать от какого-либо произвольно выбранного момента времени. Обычно рассматривают так называемую начальную фазу, которая характеризует состояние гармонического колебания в начальный момент времени, и обозначают ее буквой φ₀.

Начальная фаза колебаний вибратора в музыкальном инструменте зависит от способа его возбуждения. Так, для струны фортепиано, возбужденной ударом молотка, начальная фаза будет равна нулю, так как струна практически мгновенно начинает двигаться из своего положения равновесия. Напротив, струна щипкового инструмента, оттянутая в сторону и отпущенная, начинает свои колебания от максимального отклонения от положения равновесия, и фаза такого колебания струны будет равна не нулю, а 90°.

Теперь можно заполнить три графы «анкеты» любого гармонического колебания: частота, амплитуда и фаза. Эти параметры остаются постоянными в течение всего процесса и характеризуют колебание в целом, в отличие от переменных «отклонения у» и «времениt», характеризующих положение колеблющейся точки во времени. С учетом «анкетных данных» гармоническое колебание может быть записано аналитически в следующем виде:

у = А*Sin (ωt - φ₀), (2)

где: у — отклонение точки от положения равновесия в данный мо-
мент времени t,
А – амплитуда,
ω — круговая частота,
t – время,
φ₀ – фаза колебания (начальная фаза).

Отклонение у колеблющейся точки от положения равновесия по вышеприведенной формуле (2) можно связать с параметрами вибратора. Какие же в данном случае нужны параметры вибратора? Существует два обобщенных параметра любой колеблющейся системы, влияющие на частоту колебаний: это упругость и масса вибратора. Они обозначаются, соответственно, буквами k и m.

Коэффициент k называют еще жесткостью. Физический смысл этого коэффициента проще всего пояснить на примере пружины с грузом, который может колебаться на пружине, если второй конец пружины неподвижно закреплен в опоре: коэффициент k численно равен усилию в пружине при ее растяжении (или сжатии) на единицу длины (см). В струне коэффициент жесткости увеличивается с повышением натяжения струны, в язычке этот коэффициент можно уменьшить, подпилив язычок у основания. Выяснив теперь физический смысл упругости (жёсткости) вибратора, мы без труда поймем и связь параметров вибратора с частотой, устанавливаемую основной формулой для колебаний материальных тел:

ω = √k/m, (3)

где k и m — рассмотренные выше упругость и масса.

Значение частоты из формулы (3) можно подставить в уравнение (2). Тогда окажется, что весь процесс гармонического колебаиия зависит от четырех постоянных параметров: упругости и массы тела, с одной стороны, и амплитуды и начальной фазы – с другой. Два первых постоянных параметра выражают динамические свойства вибратора, а два последних – так называемые начальные условия колебаний (где рассматриваемая точка находилась и какую скорость имела в начальный момент времени).

Мы уже сопоставляли гармонические колебания двух камертонов при расишфровке понятия сдвига фаз, но при этом оставили без внимания реаультат совместного звучания двух камертонов, То, что случаи сложения колебаний практически имеют место в музыкальных инструментах, доказывает как опыт с камертонами, так и совместное звучание струн, язычков, пластин ксилофоиов и т. д. Например, два одновременно колеблюшихся язычка воздействуют на воздушный объём, находяшийся рядом с ними, заставляя его колебаться под воздействием суммарного движения язычков.

Рассмотрим с помощью графического сложения несколько основных случаев, характерных для настройки, а чтобы наши рассуждения были строгими, заставим колебаться два камертона или два язычка достаточно тихо с небольшими амплитудами (при больших амплитудах колебания становятся отличными от простой синусоиды) и будем поддерживать колебания в течение того времени, которое нам необходимо. В этих условиях выбранные источники звука дадут гармонические колёбания, соответствующие закону синуса. Возьмем для определенности оба камертона с одной и той же частотой, например 440 Гц. Из практики любой настройщик или музыкант знает, что результат ничего особенного представлять не будет: просто два камертона будут звучать громче, чем один. Пояснят также, что именно для увеличения громкости в фортепиано натягивают три струны, а в язычковом инструменте делают два или три язычка для одной и той же ноты.

Теория колебаний подсказывает нам, что колебания нескольких одинаково настроенных вибраторов синхронизируются, разность фаз их колебаний становится нулевой и они взаимно усиливаются. Если бы мы сложили графически две синусоиды, изображенные на схеме 5, то получили бы тоже синусоиду, с такой же частотой, но с амплитудой, равной сумме амплитуд складываемых колебаний А₁+А₂. Но теория колебаний говорит также и о том, что при сложении двух гармонических колебаний с одинаковыми частотами может происходить не только усиление колебаний, но и их ослабление. Это произойдет в том случае, если колебания антифазные, то есть с разностью фаз 180°. В этом можно убедиться, если графически сложить синусоиды, показанные на схеме 6.

Складывать необходимо с учетом направления отклонения вверх или вниз. Например, в какой-то момент времени точка в соответствии с одной синусоидой должна отклониться вверх на величину у, но в соответствии с другой синусоидой она должна отклониться вниз на ту же величину у. Если амплитуды равны, то результирующее воздействие на колеблющуюся точку оказывается равным нулю и точка должна оставаться в покое.

Теоретически два антифазных гармонических колебания с равными амплитудами взаимно уничтожаются, А₁—А₂=0. Но кто-нибудь и когда-нибудь разве слышал, чтобы два одновременно звучащих камертона гасили колебания друг друга? Нет, не слышал. Однако теория здесь права. В действительности же очень трудно при точно настроенных камертонах получить колебания с разностью фаз 180°. Колебания камертонов или струн в унисоне автоматически синхронизируются, становятся синфазными.

И все же гашение колебаний, хотя и не совсем полное, частичное, можно получить, слушая колебания одного камертона. Для этого надо расположить камертон вертикально вблизи уха и медленно вращать вокруг вертикальной оси. Нетрудно найти такое положение камертона, при котором звук как бы мгновенно пропадает. Это значит, что в данном месте на частицы воздуха действуют две гармонйческие колебательные силы, пришедшие от разных вилок и оказавшиеся в противофазе. Направление, которое соответствует линии противофазности колебаний, составляет примерно 45° к плоскости, проходящей по осям обеих вилок. Из рассмотрения этих случаев мы должны сделать два практически важных вывода: во-первых, синфазные колебания взаимно усиливают друг друга, и во-вторых, антифазные колебания взаимно уничтожают друг друга, или если амплитуды складываемых колебаний не точно равны друг другу, то уменьшаются до величины, равной разности амплитуд.

Теперь рассмотрим случай сложения колебаний, исключительно важный для практики настройки, когда в результирующем колебании периодически чередуются синфазность и антифазность складываемых колебаний. Сначала послушаем этот случай: заставим колебаться два камертона, имеющих различные частоты, например 440 и 441 Гц. Или еще проще — послушаем один тон давно не настраиваемого инструмента — пианино, баяна, одноименные двойные сгруны мандолины. При очень внимательном слушании, даже у относительно настроенного инструмента можно обнаружить хотя бы несколько тонов, в которых нет точной настройки вибраторов. На слух такое несоответствие проявляется в вибрации, дрожании тона, периодических усилениях и ослаблениях громкости звука.

В музыкальной акустике это называется б и е н и я м и. Биения легко получить в опытах с любыми источниками звуков, лишь бы два источника давали слегка различающиеся по высоте звуки. Четче всего биения проявляются на простых тонах камертонов, органных труб. В таких случаях уменьшение громкости при наступлении состояния антифазности колебаний доходит почти до нуля. Какова физическая сущность биений и как они образуются, и наконец, какова их роль в настройке? Этими вопросами мы сейчас и займемся.

Пусть два камертона 440 и 441 Гц начнут колебаться одновременно, причем разность фаз их колебаний в начальный момент будет равной нулю. Значит, какое-то время колебания камертонов будут синфазны и будут усиливать взаимно друг друга, звук в это время кажется громче. На схеме 7а показаны гармонические колебания камертонов.

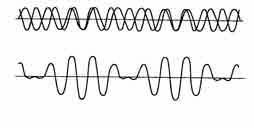
Схема 7. Сложение колебаний с небольшим различием частот, а – вверху, б – внизу

В последующие моменты времени колебания одного из камертонов, а именно имеющего частоту 440 Гц, начнут отставать от колебаний камертона с частотой 441 Гц, так что через одну секунду разница числа совершенных камертонами колебаний составит ровно одно колебание (441—440=1). Это отставание выразится в том, что через пол секунды после начала колебаний разность фаз станет равной 180°. Таким образом, синфазный участок колебания превратился, а точнее сказать, перешел в антифазный. А мы уже знаем, что противофазные колебания взаимно гасят, ослабляют друг друга.В дальнейшем опять наступает период согласованности колебаний — синфазность, и затем она снова сменяется рассогласованностью — антифазностью.

Ну а что происходит, когда колебания периодически то усиливаются, то ослабляются? Суммарное колебание в этом случае периодически становится то громче, то тише. Это и есть биения.
Графически биения представлены на схеме 7б. Амплитуда суммарного колебания в какой-то момент времени равна сумме амплитуд А₁+А₂ (период синфазности), в другой момент времени сумма амплитуд переходит в разность амплитуд А₁—А₂. В идеальном случае, когда амплитуды колебаний камертона равны А₁=А₂=А, мы можем сказать, что суммарная амплитуда периодически меняется от нуля до 2А. Когда биения слышны лучше всего? Очевидно, в этом идеальном случае равенства амплитуд складываемых колебаний: от периодов полного исчезновения звука до периодов максимальнои громкости. Хуже всего биения слышны тогда, когда одно колебание во много раз больше другого. Отсюда можно получить одно практическое правило: при настройке сравниваемые тоны должны быть по возможности равногромкими. На некоторых видах инструментов раздельная регулировка интенсивности звучания тонов вполне возможна, как, например, у рояля и пианино, и опытные настройщики этим пользуются. Соответствующим подбором силы удара по клавишам можно в некоторой степени повысить четкость биений, глубину биений.

В вышеприведенном примере, когда камертоны имели частоты 440 и 441 Гц, одно усиление или одно ослабление колебаний происходило, как было подсчитано, один раз в секунду. Так же можно подсчитать число биений в секунду и при любой другой частоте камертонов: если одновременно звучат камертоны 440 и 442 Гц, то через секунду разность количества полных колебаний камертонов достигнет 442 — 440=2, и следовательно, в течение этой первой секунды два раза произойдет совпадение и расхождение колебаний, то есть два биения. Отсюда можно получить правило для нахождения частоты биений в секунду, она равна абсолютной величине разности частот складываемых колебаний:

f _б = f ₁ – f ₂ (4)

Следовательно, чем реже биения, тем меньше разница по частоте у двух колебаний, тем точнее они совпадают друг с другом. Точная настройка в унисон будет, следовательно, при равенстве частоты биений нулю, т. е. при их отсутствии. Частоту биений не следует путать с частотой самого суммарного колебания, то есть если частота составляющих колебаний равна, например, 440 и 442 Гц, а частота биений равна разности 442 — 440=2, то какова же частота слышимого суммарного тона: 440, 442 Гц или какая-то иная? Теория колебаний доказывает, что средняя частота суммарного тона равна полусумме частот складываемых колебаний:

f = (f ₁+f ₂ )/2 (5)

Казалось бы, к чему знать эту частоту, если два звука должны быть настроены точно? Однако в некоторых случаях требуется подсчет частоты суммарного колебания, например, когда тон настраивается с биениями (розлив в язычковых инструментах). Так, средняя частота колебаний в вышеприведенном примере равна 441 Гц. Биения существенным образом влияют на качество музыкального звука. Отметим примечательную особенность колебаний с биениями: они получились в результате сложения двух гармонических колебаний, но сами не являются гармоническими, то есть синусоидальными.

Зададимся вопросом, что будет происходить с формой колебаний, если сложить еще большее число колебаний? Интуиция подсказывает, что форма колебаний должна быть сложной. Это подтверждает запись колебаний скрипичной струны Соль (схема 8).

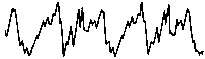
Схема 8. Форма колебаний скрипичной струны

Трудно даже сравнить кривую этого рисунка с кривой схемы 1. По форме они совсем непохожи. Единственное их сходство только в том, что они обе периодичны. Французский математик Фурье еще в прошлом веке доказал, что любое периодическое колебание может быть представлено суммой синусоидальных (гармонических) колебаний. Иначе говоря, любую сложную кривую можно разложить на ряд синусоид, что позволяет заменитъ изучение сложных по форме колебательных процессов определением параметров («анкетных данных», как говорилось выше) простейших синусоид. В связи с этим отдельное простое гармоническое колебание, входящее в состав сложного колебания, называют гармоникой.

Процесс нахождения гармоник сложной периодической кривой, которая характерна для большинства звуковых колебаний музыкальных инструментов, называется гармоническим анализом*. (Не путать с «гармоническим анализом» в теории музыки. где это понятие нмеет другой смысл.) При настройке инструмента гармонический анализ производится настройшиком на слух и заключается в том, что ухо разлагает сложные колебания, то есть анализирует музыкальный звук и выделяет из него нужные для настройки гармоники, используя биения.

Гармоники музыкального звука обладают многими интересными особеиностями, и одна из них состоит в том, что частоты гармоник имеют определенную закономерность: существует первая гармоника с самой низкой частотой f, затем имеется вторая гармоника с частотой в два раза большей, то есть 2f, дальше следует третья гармоника с частотой в три раза большей — 3f, в четыре, пять и т. д. раз большей, чем частота низшей гармоники. Первую гармонику называют основным тоном, вторую, третью и т. д. гармоники называют также первым обертоном, вторым обертоном и т. д. То есть счет гармоник на единицу выше, чем счет обертонов. Ряд частот, отношения которых соответствуют отношениям натурального ряда чисел — 1:2:3:4:5:6..., называется гармоническим рядом. Например, гармонический ряд частот от основной частоты 440 Ги будет: 440, 880, 1320, 1760, 2200... Следует сказать, что только благодаря наличию в звуке гармоник и возможен процесс настройки.

Форма периодического колебания зависит от состава гармоник, отношения их амплитуд и соотношения фаз. Стоит только изменить даже у одной гармоники амплитуду или фазу, и это повлечет изменение формы результируюшего колебания. В некоторых звуках могут отсутствовать отдельные гармоники, и это тоже отражается на форме колебания. В прошлом веке Ом установил, что для стационарных (постоянных по амплитуде) звуков фазовые соотношения сравнительно мало влияют на слуховое восприятие. Позднейшие нсследования показали, что это не совсем так и фаза гармоник в начальный момент определенным образом сказывается на тембре звука. Но до настоящего времени предпочитают при контроле физических параметров музыкального звука не вдаваться в подробности фазовых соотношений гармоник. С одной стороны, это объясняется трудностью точных измерений фаз гармоник, а с другой стороны - их влияние не настолько все же велико, чтобы его необходимо было безусловно учитывать.

Для настройщика прежде всего представляют интерес лишь частоты и амплитуды гармоник настраиваемых тонов. Совокупность гармоник с определенными частотами и амплитудами называется спектром данного колебания. Спектр обычно изображают в виде диаграммы, по горизонталыюй оси которой откладываются в масштабе (как правило, логарифмическом) номера (или частоты) гармоник, а по вертикальной оси откладывают в относительном масштабе амплитуды гармоник. На схеме 9 показан спектр звука соль скрипки. Положение каждой линии (столбика) указывает определенную частоту гармоники, а вы<