Правило комбинирования Сметса

На основе правила комбинирования Сметса комбинированные массы вероятности пересекающихся подмножеств X_i, при условии, что 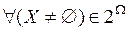, определяются выражением

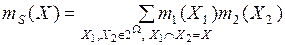. (3.14)

При этом значение m_S(Ø) соответствует значению суммарной массе вероятности, связанной с пустыми пересечениями подмножеств X_i, и определяется как

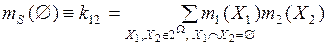. (3.15)

Рассмотрим ряд примеров, позволяющих продемонстрировать технику вычисления комбинированных масс вероятности, используя рассмотренные выше правила комбинирования свидетельств.

Пример 3.1. Пусть имеется множество альтернатив (основа анализа) 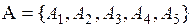и два эксперта, выполняющих их оценивание.

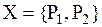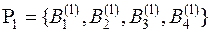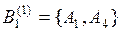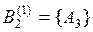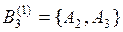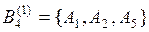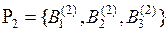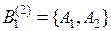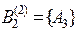В результате проведения экспертного опроса была сформирована система подмножеств , отражающая выбор экспертов 1 и 2. представляет собой множество, которое является совокупностью выделенных экспертом 1 подмножеств , , и . Экспертом 2 было сформировано множество , где , и 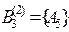. На рисунке 3.3 изображены выделенные экспертами 1 и 2 подмножества.

Рис. 3.3. Выделенные экспертами 1 и 2 подмножества (пример 3.1)

Рис. 3.4. Результирующие подмножества, образованные путем пересечения P₁ Ç P₂

Выделенным подмножествам назначены основные массы вероятности:

Эксперт 1:	;	;	;	;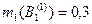
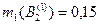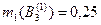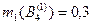Эксперт 2:	;	;	.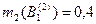

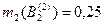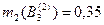В таблице 3.1 представлены результирующие подмножества, образованные путем пересечения выделенных экспертами подмножеств (P₁ Ç P₂).

Таблица 3.1