Теория свидетельств Демпстера-Шейфера (ТДШ)

В основе теории лежат следующие концептуальные положения. Пусть имеется некоторое множество 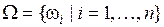, которое в теории свидетельств называется универсальным множеством или основой анализа [23,40,42]. В качестве элементов ω_i могут выступать объекты, субъекты, значения неизвестных величин, явления, события и др. Это множество является набором всех рассматриваемых утверждений (множество рассматриваемых альтернатив), и представляет собой множество исчерпывающих (всех возможных в данной ситуации) элементов и взаимно исключаемых (уникально определенных и отличных от других) элементов. При этом априори известно, что только единственный элемент ω₀ Î Ω является истинным в каждой конкретной ситуации. Этот элемент называется действительным миром.

На основе анализа Ω могут быть сформированы произвольные подмножества элементов X_i Í Ω при предположениях (свидетельствах), что действительный мир ω₀ может принадлежать каждому из этих подмножеств.

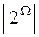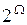Число возможных подмножеств Ω составит , где – показательное множество, совокупность всех подмножеств Ω, включая пустое множество Ø.

Свидетельствами называют любые источники информации, на основании которых могут быть получены интересующие нас оценки степеней уверенности.

Подмножества X_i, могут быть сформированы на основе системы правил:

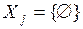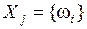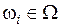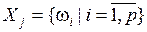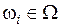1. ; 2. – экспертом выделена одна альтернатива . 3. , p < n – экспертом выделено p альтернатив . 4. 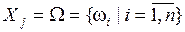– у эксперта возникли трудности с выбором (все альтернативы равноценны).

(3.1)

Таким образом, по результатам экспертного опроса может быть сформирована система подмножеств 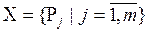, отражающая выбор всех экспертов 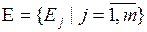, где 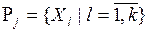– система подмножеств, сформированная экспертом E_j ( , ).

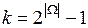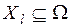Если 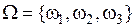, то число возможных подмножеств Ω составит 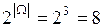. Соответственно на основе одной группы свидетельств (экспертом E_j) можно выделить следующие подмножества элементов , :

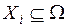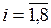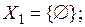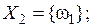
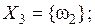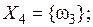
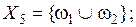
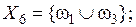
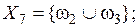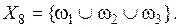
Рис. 3.1. Условное представление не перекрывающихся элементов

основы анализа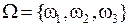

Подмножества X_i могут принимать различные формы и взаимодействовать произвольным образом (рис.3.2): X_i = {ω₁} – единичное подмножество; 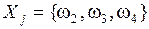– многоэлементное подмножество; X_i 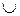X_j – объединение подмножеств X_i и X_j; X_k 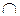X_l – пересечение подмножеств X_k и X_l и др.

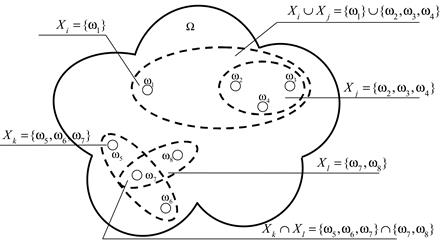
Рис. 3.2. Представление основы анализа в теории свидетельств

(теория Демпстера-Шейфера)

В основе теории свидетельств лежат три базовые функции ( ):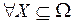

- основная масса вероятности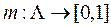

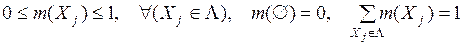; (3.2)

- функция уверенностей (доверия :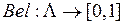

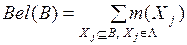; (3.3)

- функция правдоподобия :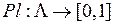

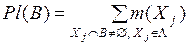; (3.4)

где 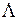соответствует .

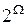Число m(X) [36,56,63] определяет субъективную степень уверенности, что искомый элемент множества Ω (так называемый действительный мир ω₀) находится в подмножестве X Ì Ω.

Значения функции уверенностей для отдельных подмножеств Ω выражают всю степень поддержки, отдаваемую каждому из таких подмножеств.

Значения функции правдоподобия для каждого из подмножеств Ω выражает полную степень потенциальной поддержки, которая может быть отдана каждому из этих подмножеств.

Значение функций Bel(·) и Pl(·) определяют верхнюю и нижнюю границы интервала, который содержит точную величину вероятности P(X) рассматриваемого подмножества X:

Bel(X) ≤ P(X) ≤ Pl(X).

Интервал [Bel(X), Pl(X)] называется интервалом доверия.

Основной процедурой, положенной в основу данной теорий, является комбинирование различных групп экспертных суждений, характеризующихся различными структурами взаимодействий.

Правила комбинирования позволяют получать агрегированные (обобщенные) экспертные оценки.

Комбинирование оценок в теории свидетельств производится на основе правила комбинирования Демпстера. При выполнении операции комбинирования могут возникать ситуации, при которых пересечение некоторых групп экспертных суждений, например, A_i и B_j может быть пустым: A_i 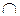B_j=Ø. Данная ситуация характеризуется наличием конфликта между экспертными оценками (суждениями, свидетельствами). Правило комбинирования Демпстера неспособно оперировать с конфликтными свидетельствами.

Попытка избавиться от этого недостатка привела к развитию альтернативных правил комбинирования свидетельств [42].

Пусть имеется универсальное множество Ω и два независимых источника данных (эксперта). Обозначим основные массы вероятности выделенных фокальных элементов, полученных из первого и второго источников, соответственно m₁(·) и m₂(·).