Основные теоретические положения диаграммы влияний

Поскольку деревья вероятностей и деревья решений не подходят для моделирования неопределённых ситуаций принятия решений в случае большого числа взаимосвязанных факторов, то получили распространения диаграммы влияний. Диаграмма влияний (ДВ) представляет собой ориентированный ациклический граф, вершины (узлы) которого отображают множество факторов задачи принятия решений. На любой ДВ выделяют следующие типы узлов [9].

Узел решений отображает множество альтернативных решений, которые на графе ДВ графически изображены в форме прямоугольников или квадратов.

Узел событий отображает множество (полную систему) неопределённых событий, которые прямо или косвенно обуславливают исходы альтернативных решений. На графе ДВ узлы событий изображаются в форме окружностей или овалов.

Узел ценности отображает функцию, по значениям которой оцениваются исходы альтернативных решений. На графе ДВ узел ценности отображается в виде ромба.

Для указанных типов узлов приняты следующие обозначения:

D – для узлов решений;

C – для узлов событий;

V – для узла ценности.

ДВ представленную в форме графа и не содержащую никакой другой информации, называют частично определённой. Для выполнения анализа решений каждый узел графа должен быть обеспечен всей относящейся к делу информацией. С каждым узлом решений связываются списки альтернативных решений. С каждым узлом событий связывается список событий и безусловные или условные вероятности их осуществления. С узлом ценности связывается список исходов всех альтернативных решений, вероятности их осуществления и значения оценочной функции. ДВ со всей относящейся к анализу информацией называют полностью определённой.

Рассмотрим некоторые общие подходы к построению ДВ [9]. Прежде всего, это подход целенаправленного генерирования ДВ, суть которого заключается в том, что путём предварительного анализа ситуаций определяется, сколько актов принятия решений и в какой последовательности необходимо осуществить для решения общей задачи. Этим самым определяется число узлов решений на ДВ. Далее определяется, каким образом будут оцениваться исходы альтернативных действий. Этим определяется узел ценности и связанная с ним оценочная функция. На основании этой информации и строится так называемая минимальная диаграмма влияний, включающая только узел (узлы) решений и узел ценности. На рис. 2.29 представлены минимальные ДВ: а) с одним узлом решений; б) с двумя узлами решений.

а) б)

Рис. 2.29. Минимальные диаграммы влияний:

а) с одним узлом решений; б) с двумя узлами решений

Далее, путём дальнейшего анализа ситуации определяются те системы неопределённых событий, которые непосредственно обуславливают исходы альтернативных решений. Узлы, отображающие эти группы событий, наносятся на граф ДВ, и дуги от них направляются в узел ценности (рис. 2.30). На рис. 2.30 представлена минимальная ДВ, дополненная узлами событий C₁ и C₂.

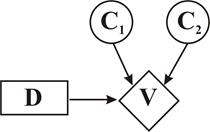
Рис. 2.30. Минимальная ДВ, дополненная двумя узлами событий C₁ и C₂

Далее производится анализ ситуации с целью выяснения того, имеются ли группы неопределённых событий, влияющих на события в уже установленных узлах C₁ и C₂.

Предположим, что было установлено существование двух таких систем неопределённых событий C₃ и C₄ (рис 2.31). События системы C₃ могут влиять на вероятности событий в узлах C₁ и C₂, а события системы C₄ – на вероятности событий в узле C₁. Узлы, соответствующие этим группам неопределённых событий, наносятся на ДВ и соединяются дугами с уже существующими узлами. Расширенная ДВ показана на рис. рис 2.31.

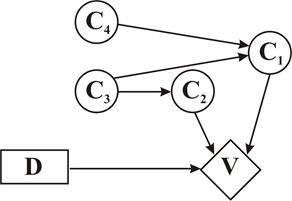
Рис. 2.31. ДВ с дополнительными узлами событий C₃ и C₄

Анализ продолжается до тех пор, пока не будут установлены все неопределённые факторы, которые могут влиять на исходы альтернативных действий. Процесс анализа задачи и построения диаграммы влияний заканчивается, когда все факторы будут учтены. После построения ДВ, необходимо выполнить её решение.

Наиболее сложной задачей при решении ДВ является расчёт вероятностей осуществления исходов альтернативных решений. Исходы альтернативных решений определяются комбинациями неопределённых событий в узлах событий – прямых предшественниках узла ценности.

Рассмотрим алгоритм решения ДВ, в основу которого положен последовательный расчёт полных вероятностей событий в узлах по всему множеству событий в узлах, прямых предшественниках этих узлов. На рис 2.32 представлена ДВ, состоящая из обуславливающих узлов событий, имеющих отношение к исходам альтернативных решений.

Поскольку узлы решений не имеют отношения к оценкам вероятностей исходов, они на рис. 2.32 не показаны.

На представленной ДВ можно выделить следующие стандартные типы связей между узлами событий:

– линейный тип связи (узлы C₁, C₂);

– расходящийся тип связи (узел C₄ и узлы C₃ и C₆);

– сходящийся тип связи (узлы C₂, C₄ и узел C₃; узлы C₄, C₅ и узел C₆).

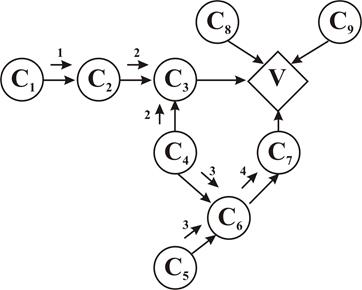
Рис. 2.32. Фрагмент условной диаграммы влияний

Рассмотрим процедуры расчёта полных вероятностей для различных типов связи узлов.

1. Линейный тип связи (рис. 2.33). Пусть с узлом C_p связаны n событий C_pi, i = 1, …, n; с узлом C_q связаны m событий C_qj, j = 1, …, m и с узлом C_r связаны k событий C_ri, i= 1, …, k.

Заданы априорные вероятности p(C_pi), i = 1, …, n, реализации событий в узле C_p, условные вероятности p(C_qj|C_pi), i = 1, …, n; j = 1, …, m реализации событий в узле C_q и условные вероятности p(C_rl|C_qj), j = 1, …, m; l = 1, …, k реализации событий в узле C_r. Полные вероятности реализации событий C_qj, j = 1, m по всему множеству событий C_pi, i = 1, …, n рассчитываются так:

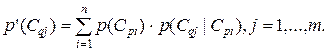(2.29)

В случае необходимости рассчитанные значения P(C_qj) нормируются, чтобы сумма значений вероятностей равнялась 1.

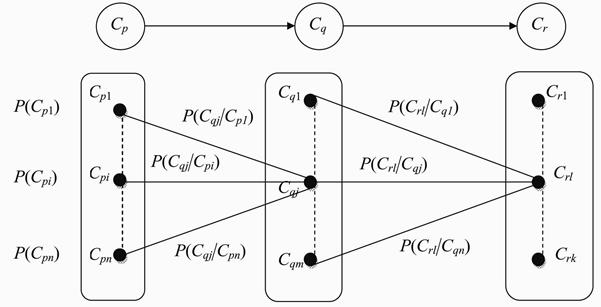
Рис. 2.33. Схема расчёта полных вероятностей для линейного типа связи между узлами событий

Теперь значения полных вероятностей принимаются за априорные вероятности и рассчитываются полные вероятности осуществления событий в узле C_r:

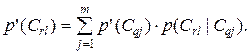(2.30)

Рассчитанные значения p’(C_rl) принимаются за априорные вероятности осуществления событий в узле C_r и в случае необходимости используются в дальнейших расчётах.

2. Расходящийся тип связей (рис 2.34). Узел C_p имеет прямыми приемниками узлы C_q и C_r. Заданы априорные вероятности p(C_pi), i = 1, …, n, реализации событий в узле C_p; условные вероятности p(C_qj|C_pi), i = 1, …, n; j = 1, …, m реализации событий в узле C_q и условные вероятности p(C_rl|C_pi), i = 1, …, n; l = 1, …, k реализации событий в узле C_r.

Поскольку события в узлах C_q и C_r условно независимы друг от друга, пока в узле C_p не произойдёт некоторое событие, а речь идёт об априорных вероятностях событий, полные вероятности событий в узлах C_q и C_r рассчитываются следующим образом:

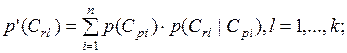
	(2.31)

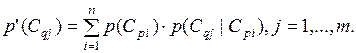
Если узел C_p имеет более двух прямых приемников, расчёт полных вероятностей осуществляется точно также.

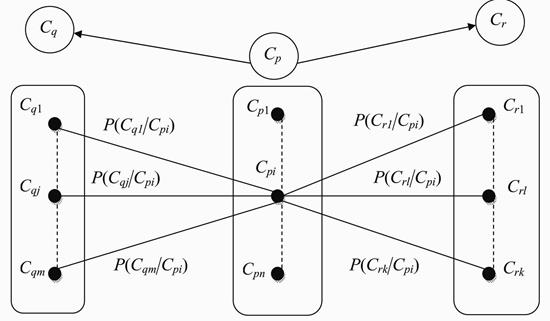
Рис. 2.34. Схема расчёта полных вероятностей для случая расходящейся связи между узлами

3. Сходящийся тип связи (рис. 2.35). Узел C_p имеет прямыми предшественниками узлы C_q и C_r. Заданы априорные вероятности p(C_qj), j = 1, …, m реализации событий в узле C_q, априорные вероятности p(C_rl), l = 1, …, k реализации событий в узле C_r и условные вероятности p(C_pi|C_qj, C_rl), i = 1, …, n; j = 1, …, m; l = 1, …, k реализации событий в узле C_p для всех возможных комбинаций событий в узлах C_q и C_r (см. рис. 2.35). Полные вероятности реализации событий в узле C_p рассчитываются по выражению:

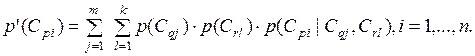(2.32)

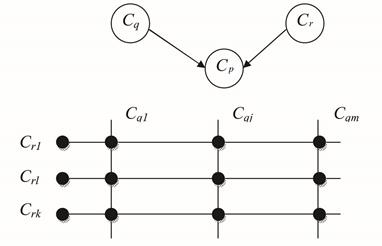
Рис. 2.35. Схема расчёта полных вероятностей для случая сходящейся связи между узлами

Такие расчёты могут быть выполнены по всей ДВ, начиная с начальных узлов и заканчивая узлами, прямыми предшественниками узла ценности. Последовательность процедур расчёта полных вероятностей для узлов диаграммы определяется структурой связей между обуславливающими узлами событий.

Так, для фрагмента ДВ, представленной на рис. 2.32, первой процедурой будет расчёт полных вероятностей событий в узле C₂ по всему множеству событий в узле C₁. Здесь имеется линейный тип связи между узлами. Далее могут быть рассчитаны полные вероятности событий в узле C₃ по всему множеству событий в узлах C₂ и C₄, поскольку имеется сходящийся тип связи. Следующей процедурой будет расчёт полных вероятностей событий в узле C₆ по всему множеству комбинаций событий в узлах C₄ и C₅. Рассчитанные полные вероятности событий в узле C₆ используются как априорные вероятности для расчёта полных вероятностей событий в узле C₇. Последовательность выполняемых процедур показана стрелками и номерами на рис. 2.32. Вместе с тем порядок процедур расчётов в общем случае произволен. Так, первой могла быть выполнена процедура 3, затем процедура 4, и только после этого процедуры 1 и 2. Также допустимы следующие порядки выполнения процедур: 1 – 3 – 4 – 2 или 1 – 3 – 2 – 4. Таким образом, порядок выполнения расчётных процедур определяется только структурой диаграммы влияний и соображениями удобства расчётов.