Боровское правило квантования круговых орбит.

В сформулированных выше постулатах Бора никоим образом не указывается способ определения стационарных орбит или параметр, отличающий эти орбиты от других. 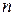В действительности Бор сформулировал признак отличия стационарных орбит от всех остальных (но обычно это положение не включают в постулаты Бора) следующим образом: момент импульса электрона находящегося на стационарной орбите должен быть кратен постоянной Планка , где - целое число.

При обосновании этого правила Бор использовал в качестве аналога постулата Планка для гармоничного осциллятора, согласно которому осуществляется только такие состояния осциллятора, энергия которых удовлетворяет условию:

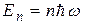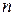, - целое число. (32.7)

Рассмотрим гармонический осциллятор, состояние которого характеризуется координатой 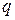и импульсом . Полная энергия такого осциллятора определяется выражением:

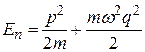(32.8)

В соответствии с постулатом Планка

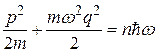(32.9)

Это выражение легко привести к виду:

(32.10)

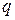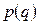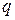Плоскость определяемую координатой и импульсом. координатами и называют фазовой. Кривую на этой плоскости , соответствующую уравнению, связывающему и , называют фазовой траекторией. Уравнение (32.10) определяет фазовую траекторию гармонического осциллятора и является уравнением эллипса с полуосям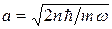и

и 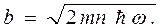(32.11)

Площадь эллипса .Поэтому

(32.12)

С другой стороны площадь эллипса на координатной плоскости , 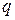можно найти по формуле

(32.13)

Приравнивая (32.12) и (32.13), получаем правило квантования в виде:

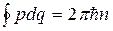(32.14)

Соотношение (32.14) есть правило квантования для гармонического осциллятора, но в обобщенной форме. Бор распространил правило (32.14) на другие механические системы, понимая под и 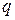обобщенные координаты, т.е. переменные, определяющие положение системы в пространстве.

Для электрона в атоме в качестве обобщенной координаты естественно рассматривать угол поворота j при его вращении вокруг ядра, а в качестве обобщенного импульса – момент импульса, связанный с его вращением - .

Поэтому условие (32.14) следует записать в виде:

(32.15)

У электрона, движущегося по круговой орбите, момент импульса остается постоянным, поэтому, вынося его за знак интеграла, получаем:

. (32.16)

Таким образом, в атоме водорода из всех возможных орбит реализуются только те, на которых момент импульса электрона кратен постоянной Планка. Это утверждение иногда все же называют третьим постулатом Бора.