Шкала взаимодействий простых подцелей
| Лингвистическое значение | Числовое (бальное) значение |
| Отсутствие взаимодействия | |
| Очень слабое взаимодействие | 0,1 |
| Слабое | 0,3 |
| Умеренное | 0,5 |
| Сильное | 0,7 |
| Очень сильное | 0,9 |
| Абсолютное взаимодействие |
3. Агрегация оценок, выбор альтернатив и подготовка рекомендаций ЛПР
С учетом сказанного, задача агрегации экспертных оценок сводится к определению интегральной оценки Qi, учитывающей влияние на Ci всех подцелей дерева. Такая оценка определяется посредством формирования матрицы (табл. 2.6) и как алгебраическая сумма вида:
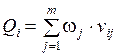 , (2.6)
, (2.6)
где ωj – вес подцели Cj; vij – экспертная оценка с учетом знака, вписанного в клетку (Ci, Cj), матрицы взаимодействия (коэффициент корреляции Ci с Cj), vij 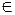 [–1,+1]. Другими словами – это алгебраическая сумма произведений значений, вписанных в клетки данной строки и значений веса из верхней строки табл. 2.6.
[–1,+1]. Другими словами – это алгебраическая сумма произведений значений, вписанных в клетки данной строки и значений веса из верхней строки табл. 2.6.
Интегральные оценки ранжируют подцели: подцель Ci тем значимее, чем больше ее оценка Qi. Это позволяет из множества отобрать наиболее существенные. С учетом результатов, полученных из табл. 2.5 выберем, например, три наиболее значимые подцели: C1.1 = (0,419) – снизить расходы на содержание и эксплуатацию оборудования; C2.1 = (0,455) – модернизировать технологии сборочно-сварочных работ; C1.3 = (0,352) – снизить общезаводские накладные расходы.
Расширим возможности рассматриваемого анализа посредством придания ему некоторой «эластичности», для чего используем элементы теории нечетких множеств. С этой целью отобранные подцели будем трактовать лингвистическими переменными, принимающими качественные значения (устанавливаемые экспертами и выражаемые вербальными формулировками типа низкий, средний, высокий и т.д.). С учетом этого для каждой выбранной подцели строим свою функцию принадлежности μ(Ci), как показано на рис. 2.4.
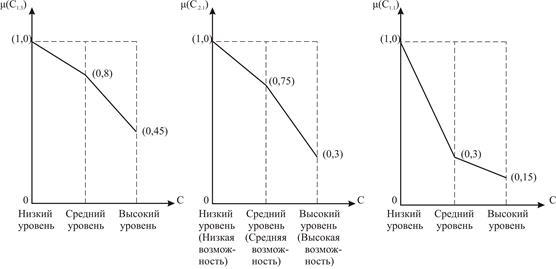
Рис. 2.4 Функция принадлежности выбранных подцелей:
а) снижение общезаводских накладных расходов; б) модернизация технологий сборочно-сварочных работ; в) снижение расходов на содержание и эксплуатацию оборудования
Здесь по оси абсцисс отложены качественные значения степени достижения подцелей, а по оси ординат – вероятности того, что это произойдет. Это позволяет сформировать ряд альтернатив (в нашем случае их 6) в виде комбинаций перестановок доминирующих подцелей (например 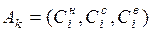 , где верхние индексы – сокращение слов «низкий», «средний», «высокий»).
, где верхние индексы – сокращение слов «низкий», «средний», «высокий»).
Наконец, для каждой альтернативы рассчитывается индекс достижимости глобальной цели (ИДЦ), равный сумме произведений интегральных оценок подцелей C1.3 , C2.1 и C1.3 на соответствующие значения функций принадлежности μ(Ci) (табл. 2.8):
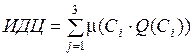 , (2.7)
, (2.7)
Таблица 2.8
Расчет индекса достижимости глобальной цели (C0)
| Альтернативы | Расчет ИДЦ | Значения ИДЦ |
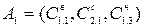
| 0,15×0,49+0,75×0,455+1,0×0,352 | 0,766 |
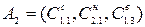
| 0,3×0,49+1,0×0,455+0,45×0,352 | 0,760 |
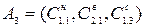
| 1,0×0,49+0,3×0,455×0,8×0,352 | 0,90 |
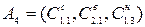
| 0,3×0,49+0,3×0,455+1,0×0,352 | 0,635 |
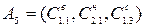
| 0,15×0,49+1,0×0,455+0,8×0,352 | 0,810 |
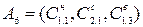
| 1,0×0,49+0,75×0,455+0,45×0,352 | 0,985 |
В результате выбирается альтернатива A6, которой соответствует максимальное значение ИДЦ=0,985, что предусматривает следующее:
– низкий уровень снижения расходов на содержание и эксплуатацию оборудования;
– средний уровень модернизации технологий;
– высокий уровень снижения общезаводских накладных расходов.
Рассмотренная технология анализа целевых сценариев предусматривает структуризацию глобальной цели, и учитывает возможные взаимосвязи подцелей на различных уровнях дерева целей. Такой подход может быть применен для решения ряда организационно-технических задач в судостроительной отрасли.
Дата добавления: 2021-03-18; просмотров: 627;











