Матрица попарных сравнений для нулевого и первого рангов иерархии

<6 7 8910 11 12 >

ω(C₀)=1	C₁	C₂	C₃	Вес цели ω
C₁				0,57
C₂	1/3			0,23
C₃	1/5	1/3		0,2
ω(C₁)=0,57	C_1.1	C_1.2	C_1.3	Вес цели ω
C_1.1				0,3
C_1.2	1/2		1/2	0,11
C_1.3	1/3			0,16
ω(C₂)=0,23	C_2.1	C_2.2	Вес цели ω
C_2.1			0,15
C_2.2	1/3		0,18
ω(C₃)=0,2	C_3.1	C_3.2	C_3.3	Вес цели ω
C_3.1				0,12
C_3.2	1/3		1/2	0,06
C_3.3	1/2			0,02

Таблица 2.5

Шкала сравнительной значимости целей

Лингвистическое значение	Числовое (бальное) значение
Одинаковая значимость целей C_i и C_j
Некоторое (слабое) преобладание значимости C_i над значимостью C_j
Существенное (сильное) преобладание C_i над C_j
Очевидное (очень сильное) преобладание C_i над C_j
Абсолютное преобладание C_i над C_j
Промежуточное значение между соседними значениями шкалы	2,4,6,8

Вес цели C_i вычисляются по формуле

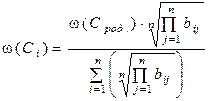, (2.5)

где ω(C_род.) – вес родительской вершины фрагмента, n – число целей нижнего уровня фрагмента дерева. Выполненные таким образом расчеты, позволяют получить набор коэффициентов (весов) значимости целей (подцелей). Упорядочив их по убыванию веса и приняв некоторое пороговое значение ω(C_i) ≥ γ (γ – некоторое значение из интервала [0,1]), т.е. γ 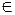[0,1], можно получить набор наиболее значимых подцелей.

Вместе с этим, для более обоснованного определения значимых подцелей, целесообразным является еще определение взаимодействий простых подцелей, представленных вершинами дерева, из которых не исходит стрелок, т.е. C_1.1,C_1.2,C_1.3 и им аналогичных. Подцель C_i взаимодействует (коррелирует) с подцелью C_j (i,j = 1…m), если достижение C_i влияет на достижение C_j. Это влияние может быть двояким: стремление к подцели C_i может способствовать либо, наоборот, препятствовать достижению подцели C_j. В первом случае на пересечении строки C_i и столбца C_j матрицы взаимодействия (табл. 2.6) проставляется знак «+», а во вором случае – знак «–».