Основные теоретические положения сетей уверенности

Основной предпосылкой появления сетей уверенностей (СУ) является сложность использования деревьев вероятностей при росте числа систем неопределенных событий: размеры деревьев растут так быстро, что становится трудно оперировать ими. Поэтому для анализа таких ситуаций были разработаны СУ, которые в последние годы находят широкое применение в теории принятия решений. Наряду с названием «сети уверенности» в литературе используются и другие альтернативные названия таких сетей: причинные сети, байесовские сети [9].

Любая СУ представляет собой ориентированный ациклический граф (ОАГ), пример которого приведен на рис. 2.9, а формальное представление выглядит так [9]: G=(V, E), где V – множество вершин; E – множество дуг. Вершины СУ называются узлами, которые обозначаются большими буквами латинского алфавита. Каждый узел отображает полную систему неопределенных событий, обозначаемых малыми буквами, соответствующими обозначению узла и индексами, отражающими порядковые номера событий.

Например факт того, что узел А содержит п событий, а узел В – т событий, представляется следующей записью:

. (2.15)

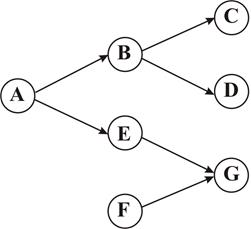
Рис. 2.9. Пример графического представления СУ

Дуга, связывающая два узла на графе, свидетельствует о том, что события в узле, из которого дуга выходит, влияют на шансы осуществления событий в узле, в который дуга входит.

Говоря о шансах наступления некоторого события, используется качественное понятие - степень уверенности в том, что данное событие произойдет. Для перевода этого понятия на количественный уровень необходимы численные оценки уверенностей, в качестве которых выступают вероятностные оценки. Эти оценки могут быть получены либо статистическими методами, если имеются необходимые данные, либо на основе экспертных суждений.

СУ представленная на рис. 2.9 не является полностью определенной, так как она задана только ОАГ. Если, кроме этого, заданы безусловные и условные, по отношению к прямым предшественникам, вероятности осуществления событий во всех узлах сети, такая СУ называется полностью определенной. Тогда выражение для ее описания примет следующий вид [9]:

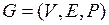, (2.16)

где V – множество вершин (узлов) ОАГ; E – множество дуг ОАГ; P – множество вероятностных оценок, характеризующих шансы наступления всех событий на сети.

Множество всех узлов, составляющих СУ характеризуется наличием следующих основных видов [9]:

1. Подмножество прямых предшественников Pd(X) некоторого узла Х образуют все узлы, из которых выходят дуги, входящие в узел Х. Например, на рис. 2.9 Pd(B)={A}, Pd(G)={E, F}, Pd(A)=Ø.

2. Подмножество прямых приемников (наследников) Sd(X) некоторого узла Х образуют узлы, в которые входят дуги, исходящие из узла Х. Для рис. 2.10 Sd(A)={B,E}, Sd(B)={C, D}, Sd(F)={G}, Sd(C)=Ø.

3. Узлы, не имеющие преемников (узлы C, D и G на рис. 2.9) называют конечными или терминальными узлами.

Все виды связей между узлом и его прямыми предшественниками и/или прямыми преемниками могут быть сведены к трем случаям [9]:

1. Линейные связи (рис. 2.10). Здесь события в узле А имеют отношение к шансам осуществления событий в узле В. В свою очередь, события в узле В имеет отношение к шансам осуществления событий в узле С.

Рис. 2.10. Линейный тип связей между узлами

2. Расходящиеся связи (рис. 2.11). В данном случае события в узле А имеют отношение к шансам осуществления событий в узлах В₁, …В_п.

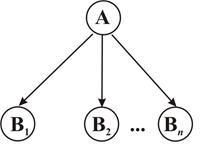
Рис. 2.11. Расходящийся тип связей между узлами

3. Сходящиеся связи (рис. 2.12). События в узлах В₁, …, В_п имеют отношение к шансам осуществления событий в узле А.

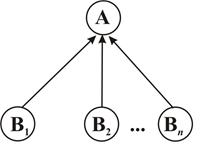
Рис. 2.12. Сходящийся тип связей между узлами

Все многообразные типы ОАГ, представляющие СУ, делятся на два больших класса [9]:

1. Односвязные ОАГ, в которых между любыми их узлами не может существовать более одного пути. Частным случаем односвязного графа является древовидный граф или дерево (рис. 2.13). Отличительной особенностью такого графа является то, что любая его вершина (узел) не может иметь более одного прямого предшественника.

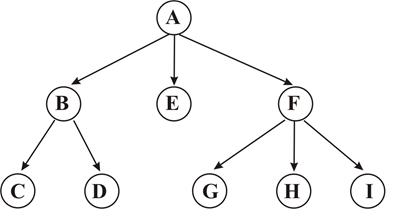
Рис. 2.13. Пример древовидного графа

Граф на рис. 2.9 не является деревом, поскольку узел G имеет двух прямых предшественников - узлы E и F. Из определения древовидного графа следует, что на нем допустимы только линейные и расходящиеся связи между узлами.

2. Многосвязные графы, на которых могут существовать множественные пути между отдельными узлами. Граф, представленный на рис. 2.14, является многосвязным, поскольку между узлами А и F существуют два пути: A®B®D®F и A®E®F.

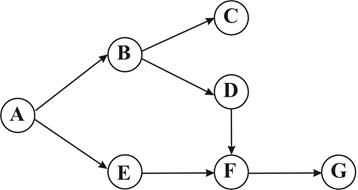
Рис. 2.14. Пример многосвязного графа

СУ строятся для моделирования сложных неопределенных ситуаций с большим числом взаимосвязанных систем событий. Основная цель, для которой строятся СУ – это решение задач вероятностного вывода, под которым понимается определение вероятностей интересующих событий на основе информации во всех узлах сети.

В самом общем виде задачу вероятностного вывода трактуют как определение вероятностей осуществления гипотез на основе наблюдений событий-свидетельств.

Понятие гипотез и свидетельств может быть относительным. Например, в качестве свидетельств может выступать некоторое множество заболеваний, а гипотезами будет множество симптомов, являющихся проявлениями этих заболеваний. Задачей вывода в данном случае будет оценка вероятностей проявления симптомов при условии наличия данных заболеваний. Может быть также рассмотрена обратная задача, когда свидетельствами являются наблюдаемые симптомы и необходимо определить вероятности гипотез – возможных заболеваний [9].

Иногда понятия гипотез и свидетельств фиксируют, и сеть уверенностей строят таким образом, что узлы (узел) с событиями гипотезами являются начальными, а с событиями-свидетельствами – конечными узлами сети. Эти узлы еще называют информационными узлами.

Естественно, что сеть может содержать любое число промежуточных узлов. Такой вероятностный вывод в направлении «гипотезы-свидетельства» называют предсказательным выводом, а вывод в направлении «свидетельства-гипотезы» - диагностическим выводом.

Простейшим типом задач вероятностного вывода является определение априорных распределений вероятностей осуществления событий в узлах сети на основе всей априорной информации, накопленной в сети. Для решения этой задачи необходима следующая исходная информация [9]:

- сформированный граф сети уверенностей со спецификацией всех событий в узлах;

- назначение всех априорных безусловных и условных вероятностей осуществления событий во всех узлах сети, например, как показано на рис. 2.15. При этом следует помнить, что вероятности осуществления событий будут безусловными только для начальных узлов сети. Для всех промежуточных и конечных узлов априорные вероятности осуществления событий будут условными.

Приведенные исходные данные позволяют решать задачу вероятностного вывода, в основе которой лежит условие наличия условных вероятностей осуществления событий только в зависимости от событий в узлах – прямых предшественниках.

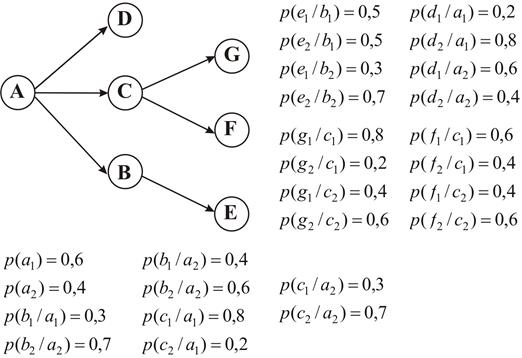
Рис. 2.15. Древовидная СУ с назначенными априорными безусловными и условными вероятностями

При этом поток распространения вероятностей выходит из начальных узлов, поочередно охватывает все промежуточные узлы и заканчивается в конечных узлах. В результате действия такого алгоритма в каждом узле рассчитывается распределение условных вероятностей, зависящее от событий во всех узлах предшественниках данного узла. Такая задача имеет прямое отношение к задачам принятия решений. Целью распространения вероятностей на сети является оценка априорных вероятностей исходов альтернативных решений.

Следует отметить, что несмотря на существование ряда достаточно строгих итерационных алгоритмов проведения расчетов на сетях уверенностей, задачи такого рода относятся к классу NP-сложных и характеризуются объемностью вычислений и экспоненциально растущим временем вывода в зависимости от размера сети уверенностей [9]. Поэтому в качестве примера рассмотрим упрощенную версию расчета распространения вероятностей на СУ посредством использования алгоритма, предложенного в работе [9].

Алгоритм предназначен для решения класса задач вероятностного вывода, в которых необходимо оценить вероятности осуществления событий на основе многих источников информации. Эти источники появляются последовательно во времени и дают оценки вероятностей с различными степенями достоверности. Формально процесс переоценки вероятностей осуществления событий при поступлении новой информации может быть представлен следующим образом. Пусть имеется группа неопределенных событий с априорным распределением вероятностей их осуществления: .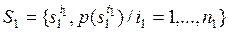

Предположим, что некоторое событие S₂ имеет отношение к шансам осуществления событий из S₁, представляются в виде вектор-столбца уверенностей:

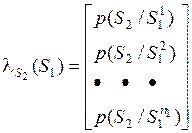. (2.17)

Пересмотренное (апостериорное) распределение вероятностей (уверенностей) наступление событий из S₁ для случая возможного наступления события S₂ может быть рассчитано на основании теоремы Байеса по следующей формуле:

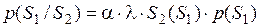, (2.18)

где p(S₁ / S₂) – пересмотренное распределение вероятностей осуществления событий из S₁; a – нормирующая константа, вводимая для того, чтобы суммаапостериорных вероятностей была равна 1; λ · S₂ (S₁) – вектор-столбец уверенностей наступления события S₂ для всех событий из S₁ (в случае, если вместо единственного события S₂ речь идет о множестве событий, вектор-столбец λ · S₂ превращается в матрицу уверенностей); p(S₁) – априорное распределение вероятностей осуществления событий из S₁. Величина λ для начальных узлов сети устанавливается равной 1 поскольку они характеризуются только безусловными вероятностями осуществления событий.