Вероятностный анализ работоспособности портовых портальных кранов с применением сетей уверенностей

Рассмотрим задачу прогнозирования работоспособности портового крана на основании результатов его диагностирования. Пусть при проведении экспертного обследования были обнаружены дефекты, представленные трещинами и разрывами определенных размеров в его несущих металлоконструкциях. На основании этого необходимо сформировать следующие рекомендации для лица, принимающего решение:

- остановка крана не производится;

- кран останавливается и выполняется его ремонт.

Предварительно выдвигаются две гипотезы, характеризующие состояние дефектов: развитие трещин и разрывов с вероятностью p₁=1 не произойдет в течении некоторого времени; с вероятностью p₂=0,3 такой процесс будет развиваться.

Для оценки уверенности того, что первое состояние дефектов будет иметь место, необходима дополнительная информация, которая может быть получена, например, из следующих источников:

1. Априорные вероятности возможных состояний дефектов могут быть получены посредством анализа отсчетов по проведению диагностики кранов одной специализированной организации. Например, анализ таких отчетов за последние 10 лет показал, что в течении 6 лет наблюдалось развитие дефектов и 4 лет их развитие не наблюдалось. Таким образом априорные вероятности интересующих нас событий равны:

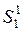– развитие дефектов не наблюдалось: ;

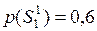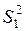– дефекты развивались: .

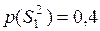2. Вторым источником информации могут быть данные, полученные от целого ряда родственных организаций, также занимающихся диагностическими работами. Пусть, исходя из данной информации, получены следующие вероятности состояний дефектов:

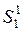– развитие дефектов не наблюдалось: ;

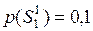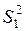– дефекты развивались: .

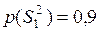3. В качестве третьего источника информации могут быть использованы результаты анализа указанных дефектов, выполненные некоторой научно-исследовательской организацией. Такие результаты, например, показатели, что подтверждаемость таких прогнозов не превышает 60%.

Всю эту исходную информацию можно использовать для строения СУ и последующего выполнения расчетов на ней (рис. 2.16).

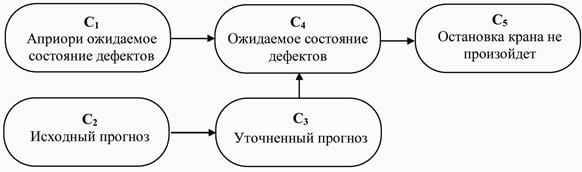
Рис. 2.16. Сеть уверенностей задачи оценивания работоспособности крана

Для отображения информации, характеризующий каждый из узлов сети строятся (формируются) соответствующие таблицы. Так например, для узлов С₁ и С₂ такие таблицы имеют вид, как показано на рис. 2.17.

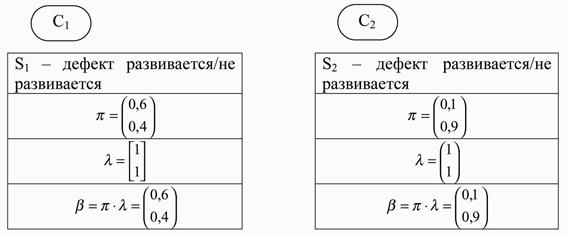
Рис. 2.17. Информация в узлах С₁ и С₂

Анализ сети начинается с этих узлов, потому что события в этих узлах являются условно независимыми от некоторых других событий. В первой строке таблицы размещается перечень событий, связанных с данным узлом.

Вектор-столбец p в следующей строке отражает начальные (априорные) вероятности осуществления событий. Вектор-столбец l в третьей строке таблицы отражает шансы наступления некоторого события (событий), имеющего отношение к событиям в данном узле. В данном случае С₁ и С₂ являются начальными узлами и для них 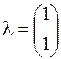, поскольку мы имеем дело только с безусловными вероятностями осуществления событий. Последняя строка таблицы отражает пересмотренные уверенности b осуществления событий в узле. В рассматриваемом случае b в каждой из таблиц просто равны начальным вероятностям p.

Поскольку события в узле С₂ влияют на вероятности осуществления событий в узле С₃, представим всю имеющуюся информацию в двух связанных таблицах (рис. 2.18).

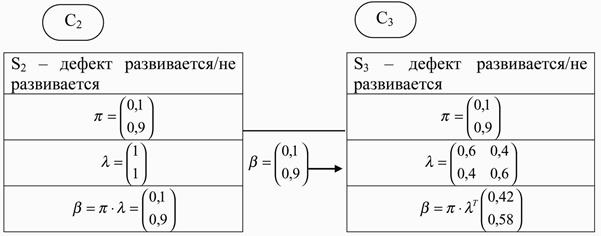
Рис. 2.18. Информация в узлах С₂ и С₃

Расчет всех необходимых данных в таблице для узла С₃ производится следующим образом. Значение b из таблицы для узла С₂ передается в таблицу для узла С₃ и выступает здесь в качестве значений начальных вероятностей p.

Матрица значений l определяется следующим образом:

Прогноз:		Ожидаемое состояние дефектов
дефект развивается	развивается	не развивается
дефект не развивается		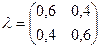(2.19)

Числа образующие матрицу l, есть не что иное, как условные вероятности ожидаемых состояний дефектов при исходном прогнозе. Они отражают только подверждаемость прогноза, равную 60%.

Для расчета уверенностей b в таблице для узла С₃ воспользуемся формулой Байеса в матричной форме:

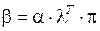
Тогда можно рассчитать вектор значений b:

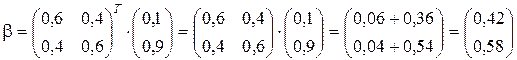. (2.20)

Определять значение нормирующей константы a нет необходимости, поскольку сумма значений b равна 1. Полученные результаты говорят о том, что на основании исходного прогноза и ожидаемой точности этого прогноза уверенность в том, что дефект будет развиваться, равна 0,42, а соответственно, уверенность в его развитии, равна 0,58.

Таким образом, имеются два источника информации об ожидаемом состоянии дефектов. Один источник – статистические данные за последние 10 лет (узел С₁), второй – исходный прогноз с учетом его достоверности (узел С₃).

Используя информацию в узлах С₁ и С₃, рассчитаем уверенности ожидаемых состояний дефектов (рис. 2.19).

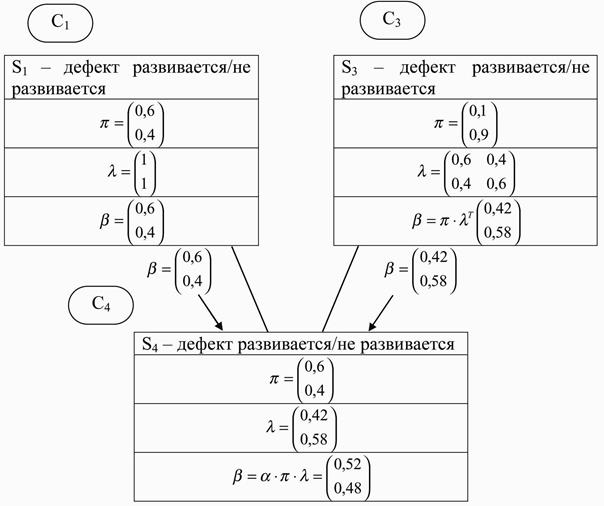
Рис. 2.19. Информация в узлах С₁, С₃, С₄

Значения b из узла С₁ транслируются в узел С₄ в качестве начальных вероятностей p. Значения b из узла С₃ транслируются в узел С₄ в качестве значений уверенностей l.

Чтобы рассчитать уверенности в узле С₄, перемножим вектор-столбцы p и l:

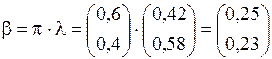; (2.21)

Для нормирования полученных значений b, рассчитаем значения нормирующей константы a следующим образом:

.

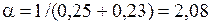Тогда нормированные значения b в узле С₄ будут равны:

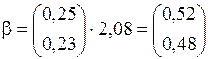. (2.22)

Теперь, когда имеется вся необходимая информация для оценки уверенности того, что дефект металлоконструкций не получит своего дальнейшего развития, рассмотрим информацию, относящуюся к узлам С₄ и С₅ (рис. 2.20).

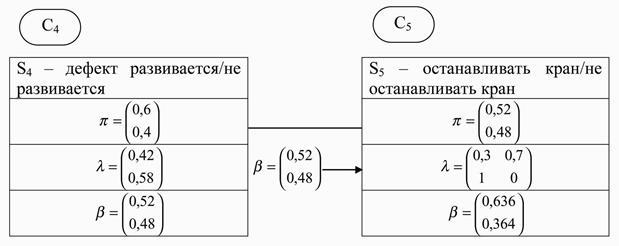
Рис. 2.20. Информация в узлах С₄ и С₅

Значения b из узла С₄ транслируются в узел С₅ в качестве значений априорных вероятностей.

Матрица l определяется на основе следующих данных:

	Дефект развивается	Останавливать кран	Не останавливать кран
Дефект не развивается	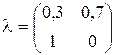;	(2.23)

Значения b в узле С₅ рассчитываются аналогично:

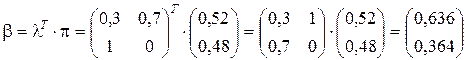; (2.24)

Таким образом, уверенность в том, что кран не придется останавливать, равна » 0,64. однако, такой результат не вполне устраивает ЛПР ответственного за данное решение.

Поэтому в качестве дополнительного источника информации, позволяющего получить новые значения уверенности, привлекаются экспертные оценки (знания). Вероятность того, что дефект не получит дальнейшего развития эксперты оценивают, вопреки исходному прогнозу, как очень высокую и равную 0,95. эксперты также уверены в своем прогнозе на 85%. Для отображения нового источника информации, преобразуем исходную сеть уверенности, как показано на рис. 2.21.

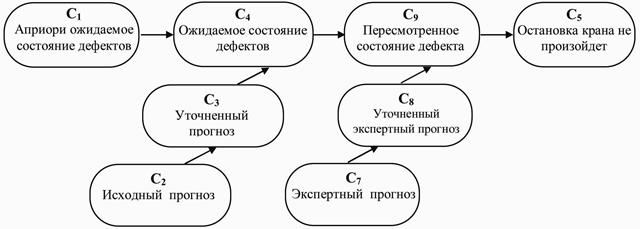
Рис. 2.21. Преобразованная сеть уверенностей

Пересчет уверенностей осуществления событий с учетом нового источника информации производится по аналогии с предыдущими расчетами, и представлен в виде таблицы на рис. 2.22 – 2.24.

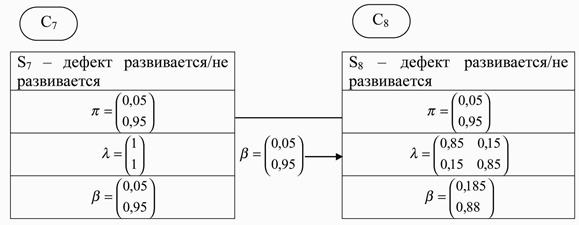
Рис. 2.22. Информация в узлах С₇ и С₈.

Рассчитаем значения b

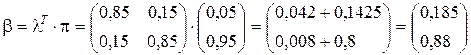; (2.25)

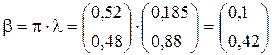. (2.26)

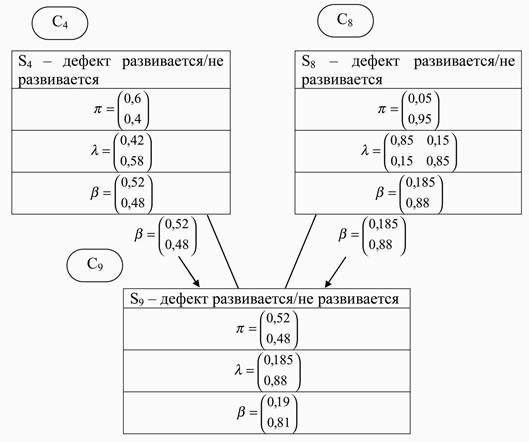
Рис. 2.23. Информация в узлах С₄, С₈, С₉

С учетом нормализации полученных значений, имеем:

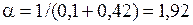
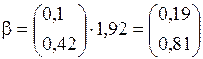. (2.27)

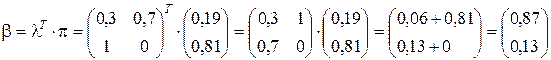. (2.28)

Привлечение дополнительной экспертной информации позволило повысить степень уверенности в том, что кран не придется останавливать с вероятностью 0,87.

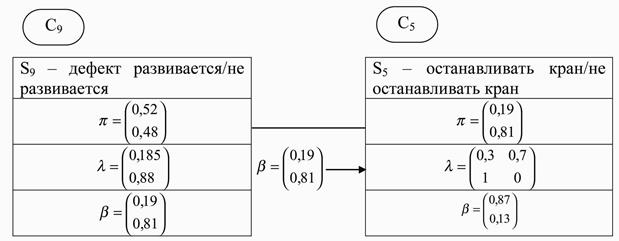
Рис. 2.24. Информация в узлах С₉, С₅

В основе приведенного алгоритма лежит идея пересчета априорных вероятностей по теореме Байеса в апостериорные вероятности с учетом информации о вероятностях осуществления событий, имеющих отношение к начальным событиям. Процесс последовательно повторяется для всей совокупности узлов на сети. Конечным результатом расчета сети являются вероятности (уверенности) осуществления интересующих нас событий в конечном узле сети.