Суммальные показатели

Средняя агрегатная - одна из форм статистической средней величины. Вычисляется по формуле

,

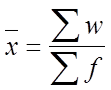где w - объемный показатель, представляющий собой произведение отдельных значений осредняемого признака ( x ) и весов ( f ), т.е. w = x f .

Например, заработная плата одного рабочего в определенных группах рабочих, умноженная на численность рабочих каждой из этих групп. Таким образом, средняя агрегатная вычисляется в тех случаях, когда известны значения числителя и знаменателя исходного соотношения средней.

Средняя степенная - общая форма представления различных средних величин, записывается как:

,

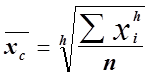где h - показатель степени;

n - число наблюдений.

При разных h получаются различные виды средних: средняя арифметическая (h = 1 ); средняя гармоническая ( h = -1 ); средняя геометрическая ( получается путем предельного перехода при h 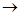0 ); средняя квадратическая ( h = 2 ) и др. Если варианты признака 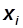представлены со своими весами f , то соответствующие средние называются средними взвешенными.

Чем больше показатель степени h , тем больше величина средней. Разница между средними тем значительнее, чем больше колеблемость осредняемого признака. При небольшой колеблемости эта разница практически мало ощутима.

Средняя арифметическая - одна из наиболее распространенных форм средней величины. Рассчитывается как частное от деления суммы индивидуальных значений (вариантов) признака на их число:

средняя арифметическая простая

;

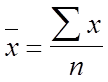средняя арифметическая взвешенная

,

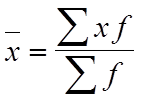где x - варианты признака;

n - число вариантов (число наблюдений), из которых рассчитывается средняя;

f - веса.

Средняя арифметическая используется тогда, когда объем варьирующего признака образуется как сумма значений признака у отдельных единиц совокупности.

Средняя гармоническая - одна из форм средней величины. Вычисляется из обратных значений признака:

средняя гармоническая простая

;

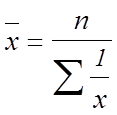средняя гармоническая взвешенная

,

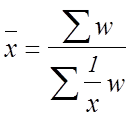где 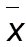- средняя величина; 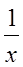- обратные значения варианта признака;

w - вес.

Средняя гармоническая применяется в тех случаях, когда непосредственные данные о весах f отсутствуют, а известны варианты осредняемого признака x и произведения значений вариантов на количество единиц, обладающих данным его значением w ( w = x f ) например, при определении средней трудоемкости продукции, средней себестоимости изделий, средней продолжительности какого-либо рода деятельности, при определении индекса цен и т.д.

Средняя геометрическая - одна из форм средней величины. Вычисляется как корень n-й степени из произведения отдельных значений - вариантов признака ( x ) :

средняя геометрическая невзвешенная

;

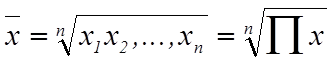средняя геометрическая взвешенная

,

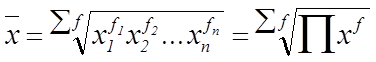где n - число значений признака;

f - вес.

Средняя геометрическая применяется, в частности, в статистических расчетах при вычислении средних темпов роста.

При определении средних величин в интервальном вариационном ряду в случае открытых крайних интервалов необходимо определить нижнюю границу первого и верхнюю границу последнего интервалов. Для этого используются величины других, закрытых интервалов: величина интервала первой группы условно принимается равной величине интервала последующей, а величина интервала последней группы - величине интервала предыдущей.

Для выбора формы средней можно воспользоваться так называемым исходным соотношением средней.

Исходное соотношение средней - соотношение двух взаимосвязанных показателей, на основании которого выбирается форма средней. Поскольку всякая средняя есть отношение, в конечном счете отношение двух величин, то выясняется, отношением каких именно величин она является в данном конкретном случае, каково ее социально-экономическое содержание. Затем это соотношение записывается словами в виде дроби (формулы). Например, требуется определить среднюю выработку рабочих в трех бригадах (табл.6.1). Средняя выработка есть отношение количества изготовленных изделий в трех бригадах к общему числу рабочих в этих бригадах. Следовательно исходное соотношение средней должно быть записано следующим образом:

средняя выработка количество изготовленных изделий

одного =

рабочего общее количество рабочих

Эта запись называется также логической формулой средней.

Таблица 6.1

Исходные данные для определения средней выработки одного рабочего

Предположим, что известны данные первых двух граф - число рабочих и количество изготовленных изделий. При сравнении исходного соотношения средней и имеющихся данных видно, что известны значения числителя и знаменателя. Чтобы вычислить среднюю величину ( 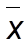) , необходимо итог гр.2 разделить на итог гр.1

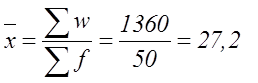шт.

Записанная формула называется средней агрегатной. Следовательно, если известны значения и числителя и знаменателя в формуле исходного соотношения средней, то средняя вычисляется по агрегатной средней.

Предположим, что известны данные о численности рабочих и выработке (гр.1 и 3). Эти данные сравниваются с исходным соотношением средней. Значения знаменателя известны, но неизвестны значения числителя, т.е. количество изготовленных изделий. Оно представляет собой произведение числа рабочих на выработку ( x f ) . Таким образом,

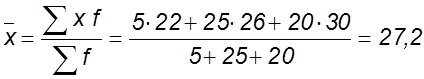шт.

Формула, по которой произведен расчет, является формулой средней арифметической взвешенной. Следовательно, если известны значения знаменателя исходного соотношения, но не известны значения числителя, средняя рассчитывается по формуле средней арифметической взвешенной.

Предположим, что известны количества изготовленной продукции и выработка (гр.2 и 3), а неизвестны значения знаменателя, т.е. численность рабочих. Она может быть получена как отношение количества изготовленных изделий и выработки ( 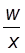) . Таким образом,

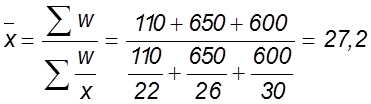шт.

Расчет произведен по формуле средней гармонической взвешенной. По всем трем формулам получено одно и то же значение средней - 27,2 шт. на человека. Это объясняется тем, что ни разу не было нарушено исходное соотношение средней, т.е. ее сущность (содержание).