Разновидности средних величин

Средняя величина(средний показатель) - это обобщенная количественная характеристика признака в статистической совокупности. Действие разнообразных факторов порождает колеблемость, вариацию осредняемого признака. Средняя величина является общей мерой их действия, равнодействующей всех этих факторов. В средней величине погашаются индивидуальные различия, вследствие этого в средней проявляется общее, закономерное, свойственное данной совокупности.

Основным условием правильного применения средней величины является однородность совокупности по осредняемому признаку. Средняя, вычисленная для неоднородной совокупности, то есть такой, в которой объединены качественно различные явления, теряет свое истинное значение. Такие средние являются фиктивными, не только не дающими представление о действительности, но и искажающими ее.

Средние величины тесным образом связаны с существом рассматриваемых общественных явлений. Они могут быть исчислены для случаев, когда каждый из вариантов вариационного ряда встречается только один раз, тогда средняя называетсяпростой илиневзвешенной, и для случаев, когда варианты или интервалы повторяются различное число раз. При этом число повторений вариантов или интервалов называетсячастотой,или статистическим весом, а средняя, вычисленная с учетом статистического веса - средней взвешенной.

В зависимости от характера статистической совокупности, осредняемых признаков и количества признаков совокупности различаются следующие средние величины: средняя генеральная, средняя выборочная, средняя групповая, средняя общая, средняя хронологическая, средняя многомерная.

Средняя генеральная- средняя величина признака в генеральной совокупности, статистический синоним понятия математического ожидания случайной величины. В качестве приближенного значения используется средняя арифметическая выборочная.

Средняя выборочная- средняя величина признака в выборочной совокупности.

Средняя групповая (частная)- средняя величина, вычисленная для отдельной группы (части) единиц совокупности. Средняя групповая характеризует типичный размер признака в группе и, следовательно, группу в целом в отношении этого признака. Средняя групповая исчисляется на основе группировки. Совокупность групповых средних конкретизирует среднюю общую (по тому же признаку) и дает более детальную характеристику всей совокупности. Средние групповые используются для выявления тенденций развития, для сравнительной характеристики групп и других целей.

Средняя общая - средняя величина, вычисленная для всей данной статистической совокупности в целом по какому-либо признаку. Средняя общая может быть вычислена как средняя из групповых средних, взвешенных по численностям групп, для которых они рассчитаны.

Средняя хронологическая - средняя величина из уровней ряда динамики (см. ряды динамики). Вычисляется для интервальных и моментных рядов. Она может быть средней невзвешенной (простой) и средней взвешенной.

Средняя хронологическая невзвешенная для интервального ряда:

;

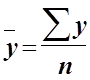где y - уровень ряда динамики;

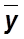- средняя из уровней ряда;

n - число уровней в ряду (число наблюдений);

для моментного ряда (с равноотстоящими уровнями):

;

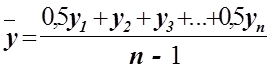Средняя хронологическая взвешенная (если известно время t , в течение которого сохранялось каждое значение y ) :

для интервального ряда

;

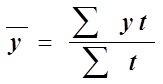для моментного ряда

,

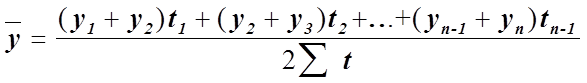где t - период времени, отделяющий один уровень ряда от другого.

Средняя многомерная - производная величина, рассчитываемая для статистической совокупности численностью n единиц с порядковыми номерами i ( i = 1, 2, 3, ... , n ), обладающих K признаками ( x ) с порядковыми номерами k ( k = 1, 2, 3, ..., K), следующим образом. Сначала вычисляются отношения 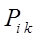значений каждого признака ( k ) у каждой единицы совокупности ( i ) к его среднему значению по формуле

,

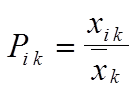где 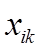- значение k -го признака у i -й единицы совокупности;

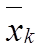- среднее значение x по k -му признаку.

Затем определяется средняя из этих отношений для каждой единицы совокупности ( 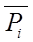), которая и называется многомерной средней

.

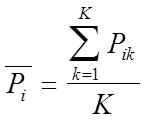Многомерные средние используются для многомерной группировки и в дальнейшем анализе данных.

Выбор вида средней необходимо согласовывать с природой реальной совокупности и признака, подлежащего осреднению. Наиболее употребительными являются суммальные и структурные (порядковые) средние. Суммальные средние разделяются настепенные, логарифмические, показательные, параболическиеи т.д. При этом степенные средние, в свою очередь, подразделяются на агрегатную, арифметическую, гармоническую, геометрическую, квадратичеcкую и т.д. К структурным средним относятся: мода, медиана, квантили, децили, процентили и др.

Наиболее часто в статистике применяются средняя агрегатная, средняя арифметическая, средняя гармоническаяи средняя геометрическая.