Первый закон термодинамики
Первый закон термодинамики есть закон сохранения энергии в применении его к термодинамическим процессам. Можно дать несколько, по существу равноценных, формулировок этого закона:
а) общая энергия изолированной системы остается постоянной независимо от каких бы то ни было изменений, происходящих в этой системе;
б) изменение внутренней энергии системы (∆U) равно разности между количеством сообщенной системе теплоты q и количеством работы А, совершенной системой.
Математическое выражение первого закона термодинамики будет иметь вид:
∆U = q - A (2.1)
q - считается положительной, если теплота поглощается системой, и отрицательной, если теплота выделяется [2].
Из первого закона термодинамики вытекает ряд следствий, имеющих большое значение для физической химии и решения различных технологических задач. Мы ограничимся применением первого закона термодинамики только для идеальных газов и рассмотрим важнейшие процессы: изохорический, изобарический, изотермический и адиабатический.
Изохорический процесс
Изохорический процесс протекает при постоянном объеме, поэтому система никакой работы не совершает. В этом случае вся теплота расходуется на увеличение внутренней энергии системы. Если V - соnst, то A=0, тогда
qV = ∆U
При изохорическом процессе количество теплоты, получаемое системой, можно вычислить по уравнениям:
qV = пСV(Т2 – T1); (2.2)
qV=nCvT1/T2(p2–p1) (2.3)
гдеn — количество вещества; р1 и р2 — соответственно начальное и конечное давление системы; — молярная теплоемкость при постоянном объеме; T1 — начальная температура; T2 — конечная температура.
Изобарический процесс
Если теплота поглощается системойпри постоянном давлении, то в системе соответственно увеличивается энтальпия. Если р = const, то
∆U = qp - А, но ∆U + А = ∆H. Тогда qp = ∆H (2.4)
Количество теплоты, получаемое системой в этих условиях, может быть вычислено по уравнениям:
qр = nСр (Т2 – T1), (2.5)
qp = 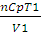 (V2 –V1) (2.6)
(V2 –V1) (2.6)
где Ср — молярная теплоемкость при постоянном давлении; V1 и V2 -соответственно начальный и конечный объем системы.
Работа при изобарическом процессе выражается уравнением:
A=р(V2 - V1) (2.7)
Изотермический процесс
Если совершается изотермический процесс, то внутренняя энергия системы при этом не меняется. Вся сообщаемая теплота расходуется на работу по расширению системы.
Если T = сonst, то ∆U = 0, тогда q = A.
Работа изотермического расширения системы может быть вычислена по уравнениям:
А = nRТ -2,3 lg 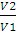 ; (2.8)
; (2.8)
A = nRТ -2,3 lg 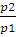 (2.9)
(2.9)
Адиабатический процесс
При адиабатическом процессе теплообмен между данной системой и окружающей средой отсутствует, поэтому q = 0. При этом система может совершать работу только за счет убыли внутренней энергии: А = -∆U. Работа в этом случае может быть вычислена по одному из следующих уравнений:
A= пСv(T1— T2), (2.10)
A = 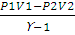 , (2.11)
, (2.11)
A = 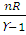 (T1 – T2), (2.12)
(T1 – T2), (2.12)
ϒ = 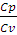 (2.13)
(2.13)
Связь между давлением, объемом и температурой в начале и конце адиабатического процесса выражается уравнениями:
p1V1ϒ = p2V2ϒ; (2.14)
T1V1ϒ-1 = T2V2ϒ-1; (2.15)
Для одноатомных газов
Cv =  R, а Cp =
R, а Cp =  R (2.16)
R (2.16)
Следовательно,
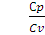 = ϒ; ϒ = 1,67 (2.17)
= ϒ; ϒ = 1,67 (2.17)
Для двухатомных газов
Cv =  R, a Cp =
R, a Cp =  R (2.18)
R (2.18)
Отсюда
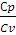 = ϒ = 1,40 (2.19)
= ϒ = 1,40 (2.19)
Примеры
1. Путем нагревания при постоянном давлении в 1,013∙105 Па газу сообщено 2093,4 Дж теплоты. Определить изменение внутренней энергии этого газа, если он при этом расширился от 0,01 до 0,02 м3.
Решение: Согласно первому закону термодинамики ∆U = q - А. Работа, совершенная газом при изобарическом расширении, может быть вычислена по уравнению (2.7):
А = р (V2 — V1);
А = 1,013 . 105 Па • (0,02 м3 - 0,01 м3) = 1013 Дж
Отсюда ∆U = 2093,4 - 1013 = 1080,4 (Дж).
2. Гелий массой 75 г нагревали при температуре 100 °С и давлении 1,013 • 105 Па. Вычислить количество затраченной теплоты, если объем газа изменился от 3 до 15 л.
Решение: Так как нагревание газа происходит изотермически и изобарически, то количество затраченной теплоты можно вычислить по уравнению (2.6), только дополнительно необходимо определить количество вещества п и молярную теплоемкость гелия при постоянном давлении:
n (Не) = 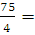 18,75 (моль)
18,75 (моль)
Гелий — одноатомный газ, поэтому согласно формуле (2.16)
Ср =  • 8,314 = 20,79 (Дж/моль);
• 8,314 = 20,79 (Дж/моль);
qp = 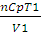 (V2 – V1)
(V2 – V1)
qp = 18,75•20,79•373/3• (15 – 3) = 581600 (Дж) или 582 кДж
3. Определить работу, совершаемую азотом при изотермическом (20 ºС) расширении его от 0,015 до 0,1 м3, если начальное давление было 3,039 • 105 Па. Каково будет конечное давление?
Решение. Для изотермического процесса работа расширения газа может быть вычислена по уравнению (2.8). Количество вещества азота находим из уравнения состояния идеального газа:
pV = nRТ;
n(N2) = 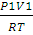 ;
;
n(N2) = 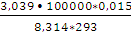 = 1,875 (моль)
= 1,875 (моль)
А = пКТ • 2,3lg 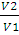 ;
;
А= 1,875 • 8,314 • 293 • 2,3 lg 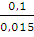 = 8657 (Дж)
= 8657 (Дж)
Конечное давление газа при постоянной температуре и известном объеме находим по закону Бойля — Мариотта:
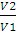 =
= 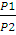
Отсюда
p2 = 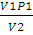 ;
;
p2 = 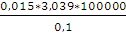 = 45600 (Па)
= 45600 (Па)
4. Сколько нужно затратить теплоты, чтобы изохорически нагреть кислород массой 25 г от 0 до 50 °С?
Решение. При изохорическом процессе газ никакой работы не совершает, поэтому вся подводимая к газу теплота расходуется на его нагревание. Согласно уравнению (2.2)
qv = nCv(T2 – T1); п (02) = 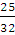 = 0,781 (моль)
= 0,781 (моль)
Для двухатомного газа
Cv =  R
R
С = 2,5 • 8,314 = 20,79 (Дж);
qv = 0,781 • 20,79 • (323 — 273) = 812 (Дж)
5. Навеску водорода массой 0,5 г, взятую при 25 °С, адиабатически сжимают от 6 до 2 л. Определить конечную температуру газа и работу, затраченную на его сжатие.
Решение. Связь между объемом и температурой адиабатического процесса показывает уравнение (2.14):
T1V1ϒ-1 = T2V1ϒ-1
Для двухатомного газа ϒ = 1,40. Из уравнения (2.14) находим Т2:
Т2 = 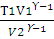 ; T2 =
; T2 = 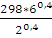
lgT2 = lg 298 + 0,4lg 6 – 0,4lg2 = 2,6651;
T2 = 462,5K
Для определения затраченной работы применим уравнение (2.10):
А = пСv (T1 — T2); п (Н2) = 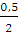 = 0,25 (моль)
= 0,25 (моль)
Для двухатомного газа Сv = 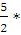 8,314 = 20,79 (Дж);
8,314 = 20,79 (Дж);
А = 0,25 • 20,79 • (298 — 462,5) = -855 (Дж)
Термохимия
Тепловым эффектом реакции называют теплоту, выделенную или поглощенную в ходе химической реакции, протекающей необратимо при постоянном давлении или постоянном объеме, причем температура исходных веществ (исх) и продуктов реакции (прод) одна и та же. В термодинамике положительной считают ту теплоту, которую подводят к системе (эта теплота поглощается системой), а отрицательной - ту, которую система выделяет. В термохимии приняты обратные обозначения.
Тепловой эффект химической реакции относят обычно к 1 моль образовавшегося вещества (обр). С этой целью нередко в термохимических уравнениях коэффициенты следует брать дробными.
Из первого закона термодинамики (2.1) следует: qv = ∆U; qv = ∆H. Таким образом, тепловой эффект химической реакции при постоянном объеме представляет собой изменение внутренней энергии системы ∆U , а при постоянном давлении — изменение энтальпии ∆H . Разница между∆H и ∆U мала, если реакция идет между жидкими или твердыми веществами. В случае реакций с участием газообразных веществ это различие заметно. Если в реакции участвует п1 моль, а получается п2 моль газообразных веществ, то
∆H = ∆U +RT (n2 — n1) (2.20)
В термохимии чаще имеют дело с ∆Н.
Основным законом термохимии является закон Гесса (1840) — частный случай первого закона термодинамики: если процесс идет при постоянном давлении или при постоянном объеме, то тепловой эффект химической реакции зависит только от начального и конечного состояния реагирующих веществ и не зависит от пути, по которому реакция протекает. Из закона Гесса вытекают следствия:
1. Тепловой эффект химической реакции равен разности между суммой теплот образования получающихся веществ и суммой теплот образования вступающих в реакцию веществ (с учетом их стехио- метрических коэффициентов):
∆Нреакц = ∑(∆Нобр)прод - ∑(∆Н обр)исх (2. 21)
2. Тепловой эффект химической реакции равен разности между суммой теплот сгорания (сгор) исходных веществ и суммой теплот сгорания продуктов реакции (с учетом их стехиометрических коэффициентов):
∆Нреакц = ∑(∆Hсгор)исх - ∑(∆Hсгор)прод (2.22)
Величины стандартных теплот образования и теплот сгорания находят в справочниках. Значение закона Гесса состоит в том, что он позволяет определить тепловые эффекты таких реакций, которые или нереализуемы, или не могут быть проведены чисто, т. е. без побочных процессов [2].
При растворении кристаллогидратов наблюдается более низкий тепловой эффект, чем при растворении безводной соли. Разность между теплотой растворения безводной соли ∆Hбезв и теплотой растворения ее кристаллогидрата ∆Hкр есть теплота гидратации ∆Hгидр:
∆Нгидр = ∆Нбезв - ∆Нкр (2.23)
Примеры
1. Реакция горения ацетилена при стандартных условиях выражается уравнением:
С2Н2 + 2  02 = 2С02+ Н2Ож, ∆Н = -1300 кДж
02 = 2С02+ Н2Ож, ∆Н = -1300 кДж
Определить теплоту образования ацетилена при постоянном давлении.
Решение. Для решения задачи данный химический процесс следует разбить на отдельные промежуточные стадии:
1) разложение ацетилена на углерод и водород:
С2Н2 = 2С + Н2 + ∆ Нх
2) образование углекислого газа из углерода и кислорода:
2С + 202 = 2С02 - 2 • 393,77 кДж
3) образование жидкой воды из водорода и кислорода:
Н2 +  02 = Н2Ож - 285,96 кДж
02 = Н2Ож - 285,96 кДж
Сумма тепловых эффектов всех стадий этого процесса и должна равняться общему тепловому эффекту горения ацетилена:
∆ Нх - 787,54 - 285,96 = - 1300
∆Нх = -226,5 кДж, ∆Нх - теплота разложения ацетилена; следовательно, теплота образования ацетилена при стандартных условиях ∆Нº298 равна 226,5 кДж.
Теплоту образования ацетилена также можно определить, используя следствие из закона Гесса (2.21), т. е. теплота горения ацетилена будет равна сумме теплот образования 2 моль углекислого газа и 1 моль воды (жидкой) минус теплота образования 1 моль ацетилена:
-2 • 393,77 - 285,96 - ∆Нº298 = -1300;
∆Нº298 = 226,5 кДж
2. Процесс алюминотермии выражается химическим уравнением:
8А1 + ЗFe304 = 4А1203 + 9Fe + ∆Н
Рассчитать, сколько выделится теплоты при сгорании 1 кг термита.
Решение. По теплотам образования участвующих в реакции веществ определим тепловой эффект реакции в целом. Для этого рассмотрим отдельно каждую стадию процесса:
1) ЗFе304 = 9Fе + 602 + 3 • 1117,82 кДж;
2) 8А1 + 602 - 4А1203 - 4 • 1670,5 кДж.
Алгебраическая сумма всех стадий процесса и будет составлять тепловой эффект реакции:
∆H = 3 • 1117,82 — 4 • 1670,5 = -3328,5 кДж
Из уравнения реакции следует, что 3328, 5 кДж теплоты выделяется при взаимодействии алюминия массой 216 г (8 • 27) и магнетита массой 696 г (3 • 232), т. е. при сгорании термита массой 912 г. При сгорании термита массой 1000 г выделится х кДж:
912 : 1000 = -3328,5 : х; х = -365 (кДж)
3. Вычислить тепловой эффект при постоянном давлении и постоянном объеме в стандартных условиях реакции:
С2Н5ОНж + 02 = СН3СООНж + Н2Ож
Решение. Тепловой эффект реакции может быть рассчитан по теплотам образования участвующих в реакции веществ (2.21). Но в данном случае удобнее его рассчитать по тепловым эффектам сгорания (2.22). В справочнике находим тепловые эффекты полного сгорания всех реагирующих веществ в кислороде. Теплота сгорания этилового спирта равна — 1367,7 кДж. Теплота сгорания СН3СООНж равна — 872,1 кДж. Теплота сгорания Н2Ож равна нулю, так как она высший оксид, продукт полного сгорания водорода в кислороде:
∆Нреакц = - 1367,7 - (-872,1) = - 495,6 (кДж/моль)
∆Uº289 рассчитываем по уравнению (2.20), но предварительно килоджоули переведем в джоули:
∆Uº289 = -495600 – 8,314 • 298 • (0 - 1); ∆Uº289 = - 493 (кДж)
4. На сколько градусов повысится температура при растворении 0,5 моль серной кислоты в воде массой 400 г, если теплота растворения серной кислоты равна — 74,94 кДж, а удельная теплоемкость раствора равна 3,77 Дж/(г • К)?
Решение. 74 940 Дж выделяются при растворении 1 моль кислоты. При растворении же 0,5 моль серной кислоты массой 49 г в воде массой 400 г образуется раствор массой 449 г и выделится 37 470 Дж (74 940 • 0,5). 3,77 Дж нагревают раствор массой 1 г на 1 °С, а 37 470 Дж нагревают на ∆t:
449 • 3,77 • ∆t = 37 470. Отсюда ∆t = 22,14 °С.
5. При растворении сульфата меди массой 8 г в воде массой
192 г температура повышается на 3,95 °С. Определить теплоту гидратации сульфата меди СuS04, если известно, что теплота растворения СuS04,• 5Н20 равна 11 723 Дж. Удельная теплоемкость раствора равна 4,187 Дж/(г • К).
Решение. Для нагревания раствора массой 1 г на 1 °С потребуется 4,187 Дж, а для нагревания раствора массой 200 г (8 + 192) на 3,95 °С потребуется:
4,187 • 200 • 3,95 = 3308 (Дж)
Следовательно, при растворении сульфата меди массой 8 г в воде массой 192 г выделяется 3308 Дж, а при растворении 1 моль (160 г) безводной соли выделится ∆Hбезв.
Тогда 8:160 = -3308:∆Hбезв;
∆Hбезв=-66160 (Дж).
Из уравнения (2.23) находим теплоту гидратации:
∆Нгидр = 66160 - 11723 = - 77 883 (Дж)
Дата добавления: 2016-12-09; просмотров: 3740;











