Второй закон термодинамики

Согласно второму закону термодинамики теплота самопроиз­вольно может переходить только от более нагретого тела к менее нагретому. Установлено, что в работу может превращаться только часть той теплоты, которая переходит от нагревателя к холодиль­нику, и тем большая, чем больше разность температур:

A = q 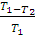(2. 24)

где q - теплота, отдаваемая нагревателем; T₁—температура на­гревателя; Т₂ — температура холодильника.

Отношение называется коэффициентом полезного действия (КПД) - η. Отсюда

η = 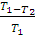(2.25)

На основе второго закона термодинамики Клаузиус ввел поня­тие энтропии S — термодинамической функции системы. Измене­ние энтропии ∆S в каком-либо процессе зависит только от начального и конечного состояний системы и не зависит от пути перехода.

Наиболее просто ∆S определяется для обратимых неизолирован­ных изотермических процессов:

∆S = (2.26)

где q — количество теплоты, сообщенное системе.

При изотермическом плавлении или испарении количества ве­щества 1 моль: ∆S = ∆H/T

где ∆H - теплота плавления или теплота испарения.

Если происходит изотермическое расширение п моль идеального газа, то

∆S =nR • 2,3lgV₂/V₁ (2.28)

∆S = nR2,31gp₁/p₂ (2.29)

Если же в системе, состоящей из идеального газа, изменяется одновременно несколько параметров, то

∆S = пС_v . 2,3lgT₂/T₁+ пR • 2,3 lgV₂/V₁ (2.30)

∆S = пС_p • 2,3lgT₂/T₁ + пR ∙2,3lg p₁/p₂ (2.31)

∆S = п • 2,3(C_vlg p₂/p₁ + C_plg(V₂/V₁) (2.32)

Вычисление ∆S в необратимых процессах ведут по уравнениям для процессов обратимых. Это вполне закономерно, так как изме­нение энтропии при заданном начальном и конечном состояниях системы не зависит от пути перехода и, в частности, от обратимости процесса. Если необратимый и обратимый процессы проводятся в одних и тех же граничных условиях, то
∆S_oбр =∆S _неoбр.[2].

Примеры

1. К котлу с водой, находящейся при 100 °С, подвели 8374 Дж теплоты. Найти КПД и максимальную работу, которую можно получить от котла, если температура холодильника 30 °С.

Решение. Максимальную работу находим по уравнению (2.24):

А ₌ q(T₁ – T₂/T₁);

A = 8374 • (373 – 303)/373 = 1571 (Дж)

Согласно уравнению (2.25)

η = ;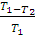

η ₌ 373-303/373₌ 0,1875, или 18,75 %

2. При временном контакте тела с температурой 200 °С с телом, нагретым до 100 °С, перешло 418,7 Дж теплоты. Найти общее изме­нение энтропии системы.

Решение. Изменение энтропии теплоотдатчика и теплоприемника находим по уравнению (2.26):

∆S₁ =q/T;

∆S₁ = -418,7/473 = - 0,885 (Дж)

∆S₂ = 418,7/373 = 1,122 (Дж)

Находим общее изменение энтропии:

∆S = ∆S₁ +∆S₂; ∆S = -0,885+1,122 = 0,237 (Дж)

3. Азот объемом 0,001 м³ смешан с кислородом объемом 0,002 м³ при 27 °С и давлении 1,013 • 10⁵ Па. Найти общее изменение энтро­пии системы.

Решение. При смешении газы будут диффундировать друг в друга. Межмолекулярным взаимодействием газов можно пренеб­речь, так как при данных условиях газы можно принять за идеаль­ные. Поэтому общее изменение энтропии при смешении газов будет равно сумме изменений энтропий каждого газа при его расширении до объема смеси. Так как процесс изотермический, то из уравне­ния (1.28) для каждого газа

Из уравнения (1.8) n =pv/RT;

n(N₂) = 0,001•1,013•10⁵ = 0,0405;

n(O₂) = 0,002•1,013•10⁵/8,314•300 = 0,081;

∆S(N₂) = 0,0405 • 8,314 • 2,3lg(0,003/0,001) = 0,371 (Дж)

∆S(O₂) = 0,081• 8,314 • 2,3lg(0,003/0,002) = 0,274 (Дж)

∆S = 0,371 + 0,274 = 0,645 (Дж)

Эта задача может быть решена и по уравнению (2.29), нужно только по уравнению (2.11б) найти парциальные давления газов:

p(N₂) = p_об ;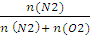

p(N₂) = 1,013 • 10⁵ +0,0405/0,0405 + 0,081 = 0,337 * 10⁵ (Па);

p(O₂) = 1.013•10⁵ – 0,337•10⁵=0,676•10⁵ (Па);

∆S(N₂) = 0,0405•8,314•2,3lg(1,013•10⁵/0,337•10⁵)=0,371 (Дж);

∆S(O₂) = 0,081•8,314•2,3lg(1,013•10⁵/0,676•10⁵)=0,274 (Дж);

∆S = 0,371+0,274=0,645 (Дж);

4. Вода массой 1 кг, взятая при 0 °С, переведена в состояние перегретого пара с температурой 200 °С и давлением 101,3 кПа. Вычислить изменение энтропии этого перехода, если удельная теп­лота испарения воды при 100 °С равна 2257 Дж/г, удельная тепло­емкость воды равна 4,187 Дж (г•К), а удельная теплоемкость водяного пара при давлении в 1,013 • 10⁵ Па равна 1,968 Дж (г•К).

Решение. Общее изменение энтропии будет складываться из трех составляющих: изменения энтропии ∆S₁ при нагревании воды до температуры кипения, изменения энтропии ∆S₂ при пере­ходе воды из жидкого состояния в парообразное и, наконец, изме­нения энтропии ∆S₃ при нагревании сухого пара от 100 до 200 °С: ∆S = ∆S₁+∆S₂ + ∆S₃

∆S₁ определяем по уравнению ∆S = пС_р • 2,3lg(T₂/T₁) —. Оно получено из уравнения (II, 31), если предположить, что система под­чиняется законам для идеальных газов и что объем воды при на­гревании не изменяется. Молярная теплоемкость С_р равна удель­ной теплоемкости, умноженной на молярную массу: С_р = 4,187 • 18 = 75,4 (Дж/(моль • К);

п (Н₂0) = 1000 : 18 = 55,6 моль;

∆S₁ = 55,6 • 75,4 • 2,3lg(373/273) = 1305,5 (Дж)

∆S₂ находим по уравнению (II, 27). Молярная теплота испаре­ния равна:

∆H_исп = 2256,7 • 18 = 40 620 (Дж/моль);

∆S_{2 =} ∆H_исп/T; ∆S_{2 =} 55,6 • 40 620/373 _{= 6065} (Дж)

При нагревании сухого пара от 100 до 200 °С при постоянном давлении изменение энтропии равно: ∆S₃ = пС_р • 2,3lg(T₂/T₁). Молярная теплоемкость пара С_р = 1,968 • 18 = 35,42 (Дж/моль).

∆S₃ = 55,6 • 35,42 • 2,3lg(473/373) = 464,3 (Дж);

∆S = 1303,5 + 6055 + 464,3 = 7824,8 (Дж)