Неразвертывающиеся линейчатые поверхности с двумя направляющими

К ним относятся поверхности с плоскостью параллелизма (поверхности Каталана).

Линейчатые поверхности с двумя направляющими (m, n) - у которых образующая прямая линия (l) в каждый момент движения, пересекая направляющие, остается параллельной некоторой неподвижной плоскости, называемой плоскостью параллелизма.

Различают три вида таких поверхностей:

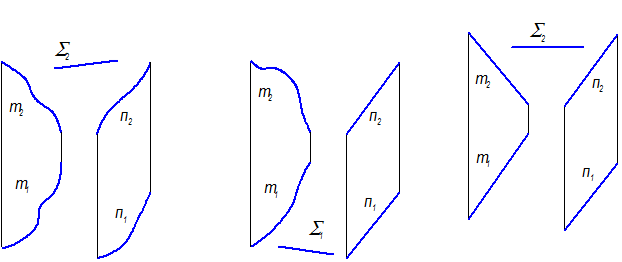
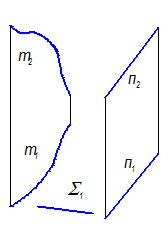
1. Цилиндроид - если направляющими являются две кривые линии (плоские или пространственные) (рис. 2-63, 2-64)

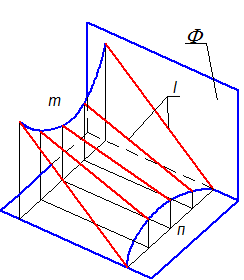
Рис. 2-63

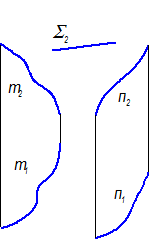
Цилиндроид

Рис. 2-64

2. Коноид - если одна из направляющих- прямая линия, а вторая - кривая (2-65).

Коноид

Рис. 2-65

3. Гиперболический параболоид (косая плоскость) - если обе направляющие - прямые линии (2-66).

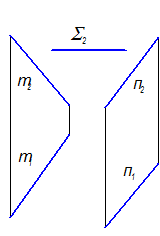
Гиперболический параболоид

Рис. 2-66

Цилиндроид

Алгоритм построения цилиндроида

Для построения образующих (если поверхность уже сконструирована) проводят ряд плоскостей, параллельных плоскости параллелизма, и определяют точки их пересечения с направляющими (m, n) (Рис. 2-67).

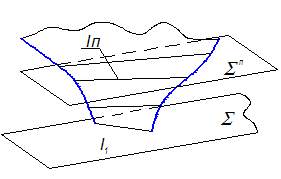
Рис. 2-67

Для удобства построения часто за плоскость параллелизма принимают одну из плоскостей проекций; тогда образующие становятся линиями уровня.

Задача: сконструировать поверхность Ф - цилиндроид, М Ì Ф, М₁ = ?

1. Задать проекции элементов определителя: Ф(m, n, П₁) (Рис. 2-68) ;

2. Построить проекции поверхности - дискретный каркас из пяти образующих:

l Ç m, l Ç n, l || П₁

Задать проекции элементов определителя m(m₁, m₂); n(n₁, n₂).

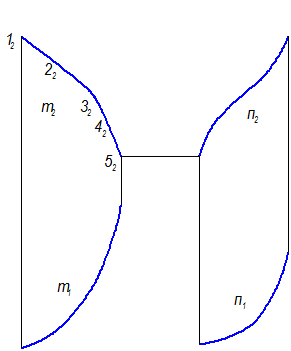
Рис. 2-68

а) На m₂, например, взять 5 точек (но чем больше, тем точнее построение поверхности) (1₂, 2₂, 3₂, 4₂, 5₂) (рис. 2-69);

б) Через эти точки провести пять l || П₁ Þ 6₂, 7₂, 8₂, 9₂, 10₂ (рис. 2-70), все l₂ ^ линиям связи, т.е. образующие занимают положение горизонталей.

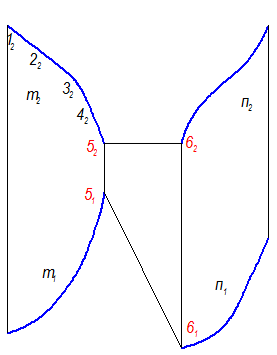
Рис. 2-69

в) Построить горизонтальные проекции этих точек на m₁ и n₁

г) Построить горизонтальные проекции образующих, соединяя:

1₁-10₁; 2₁-9₁; 3₁-8₁; 4₁-7₁; 5₁-6₁ (рис. 2-70).

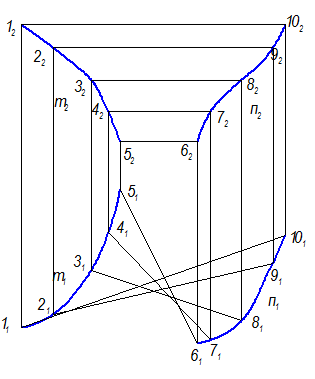
Рис. 2-70

3. Линиями обреза являются образующие 1-10, 5-6.

4. Определить видимость (рис. 2-71).

а) Относительно П₂ все образующие видимы.

б) Относительно П₁: образующая 1₂10₂ выше всех, поэтому она видима на П₁. Другим способом: точки А и В - горизонтально конкурирующие. Обвести проекции поверхности плавной огибающей кривой, учитывая, что это линейчатая, но кривая поверхность.

5. Для построения М₁ необходимо провести дополнительную образующую

C₂D₂ ® C₁D₁, М₁ Î C₁D₁.

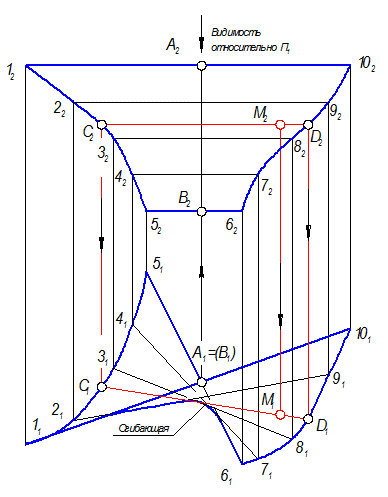
Рис. 2-71

Проекции коноида (рис. 2-72) и гиперболического параболоида (рис. 2-74) строятся аналогично цилиндроиду

Коноид

Т (m, n, П₂)

М(М₂) Î Т, М₁ =?

Закон каркаса: l Ç m, l Ç n (n ^ П₂), l || П₂,

Рис. 2-72

Задать проекции элементов определителя m(m₁, m₂); n(n₁, n₂).

n - фронтально проецирующая прямая.

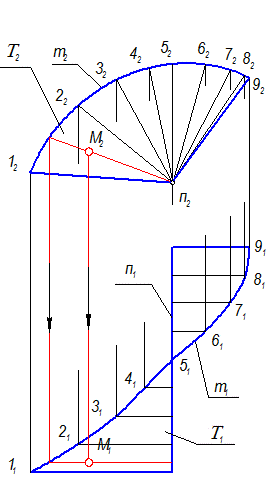
Рис. 2-73