Гиперболоид вращения

Образуется вращением гиперболы вокруг её оси.

Различают однополостный и двуполостный гиперболоиды вращения.

Однополостный (рис. 2-89) образуется при вращении гиперболы вокруг мнимой оси (рис-2.90). Поверхность однополостного гиперболоида может быть образована и вращением прямой линии вокруг скрещивающейся с ней оси (рис. 2-91).

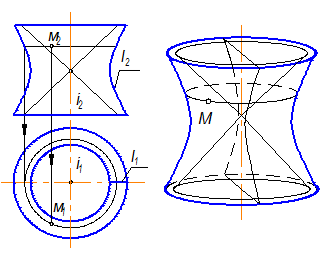
Рис. 2-89

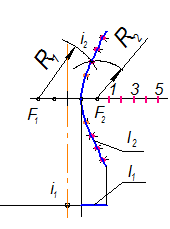
Определитель однополостного гиперболоида S (l, i ^ П₁)

Рис. 2-90

Определитель однополостного гиперболоида (образующая - прямая линия). Образующая и ось скрещивающееся прямые. Эту поверхность относят и к линейчатым поверхностям

S (l, i ^ П₁, l ° i) (рис. 2-91).

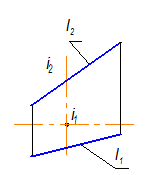
Рис. 2-91

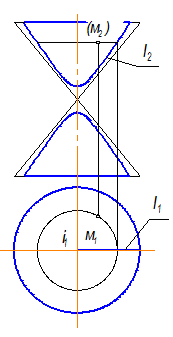
Двуполостный гиперболоид вращения образуется при вращении гиперболы вокруг ее действительной оси.

Рис. 2.93.

Один из способов (рис. 2-92) построения однополостного гиперболоида: т.к. горизонтальные проекции всех образующих должны касаться проекции горловой окружности, то каждое последующее положение прямолинейной образующей можно создавать проведением касательных к проекции окружности горла.

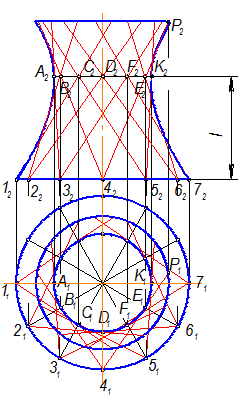
Рис. 2-92

Выдающийся русский инженер В.Г. Шухов (1921г) предложил использовать однополостный гиперболоид для строительства прочных и технологичных конструкций (радиомачт, водонапорных башен, маяков).

Алгоритм построения, если поверхность задана параллелями и расстоянием (l) от экватора до горла (рис. 2-92):

1. Разбить горловую (А,В,С...) и нижнюю (1,2,3,..) параллели на 12 равных частей;

2. Из точки 4₁ провести образующие так, чтобы они были касательными к горловой параллели (т.е. через В₁ и Е₁), на горизонтальной проекции верхней параллели получим точку Р₁, которая определит положение верхней параллели на фронтальной проекции. Эти образующие и на П₂ пройдут через те же точки (4₂, В₂, Е₂).

3. Для остальных точек построение повторить.

Только три поверхности вращения второго порядка имеют в качестве образующей прямую линию. В зависимости от расположения этой прямой относительно оси, можно получить три вида линейчатых поверхностей вращения второго порядка:

1. цилиндр, если образующая параллельна оси вращения x² + y² = R²;

2. конус, если образующая пересекает ось вращения k²(x² + y²) – z² = 0;

3. однополостный гиперболоид вращения, если ось и образующая скрещиваются

(x² + y²) / a² – z² / d² = 0