Поверхности вращения второго порядка

Цилиндр вращения

Цилиндр вращения образуется вращением образующей- l(прямой линией) вокруг параллельной ей оси.

Г(i.l), а(а₂) Ì Г; а₁, а₃ =?

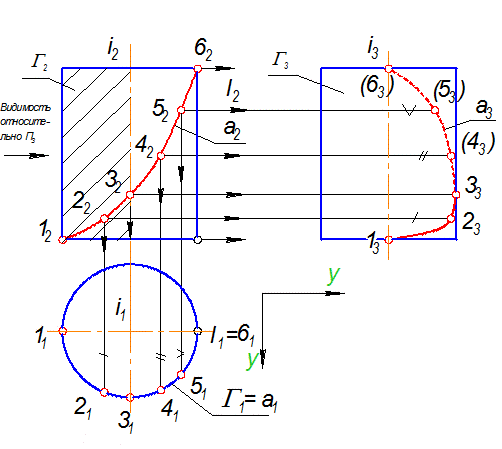
Рис. 2-81

Алгоритм построения

1) i ^^ П₁, l || i, l - горизонтально проецирующая прямая, значит Г ^^ П₁ -цилиндр занимает проецирующее положение относительно П₁.

2) Г₁ - главная проекция, которая обладает собирательными свойствами, поэтому а₁ = Г₁,

3) а₃ строится по свойству принадлежности линии данной поверхности (а Ì Г) (см. рис. 2-81)

4) Точка 3 расположена на профильном меридиане, поэтому точка 3₃ является границей видимости на П₃

Конус вращения

Конус вращения образуется вращением образующей- l (прямой линией) вокруг оси, которую она пересекает.

F(i, l), a(а₂) Ì F; а₁, а₃ = ?

i ^ П₁, l Ç i; l - занимает положение прямой уровня (фронтали)

l- прямая линия, поэтому цилиндр и конус относят так же и к линейчатым поверхностям. Например, конус можно задать другим способом, как линейчатую поверхность F(m,S), S - фиксированная точка, m (окружность, основание конуса) - неподвижная направляющая. Или как циклическую поверхность F(m,l), у которой l-образующая есть монотонно меняющаяся окружность, движущаяся по неподвижной направляющей (прямой линии) -m.

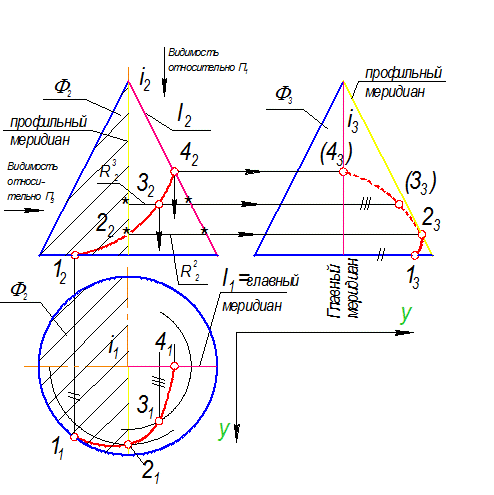
Рис. 2-82

Алгоритм построения а₁, а₃

1. Сначала отмечают на а₂ особые точки (рис. 2.82):

Точка 1₂ Þ 1₁, 1₃ - по принадлежности окружности основания

Точка 4₂ Þ 4₁, 4₃ - по принадлежности главному меридиану

2. Промежуточные: 3₂ Þ 3₁, 3₃ по принадлежности параллели радиусом – R₂³

3. Точка 2₂ Þ 2₁ по принадлежности параллели – R₂²

2₂ - 2₃ по принадлежности профильному меридиану

Видимость кривой - а:

1) На П₁ кривая а₁ видима, т.к. на П₁ видима вся поверхность.

2) На П₃границей видимости служит профильный меридиан (точка 2₃).

Сфера

Сфера образуется вращением окружности (l) вокруг оси (ее диаметра) (i)

Г(i l), - сфера, i ^ П₁ А(А₂) Î Г; А₁, А₃ = ?

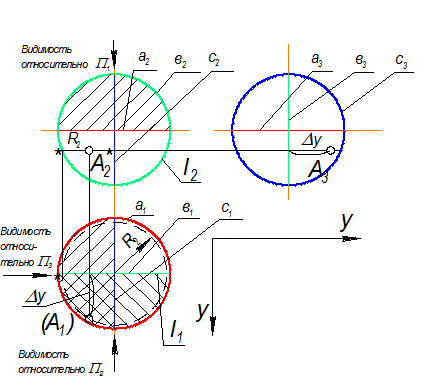
Рис. 2-83

а (а₁, а₂, а₃) - экватор, определяет видимость относительно П₁

в (в₁, в₂, в₃) - главный (фронтальный) меридиан, определяет видимость относительно П₂

с (с₁, с₂, с₃) - профильный меридиан, определяет видимость относительно П₃

Алгоритм построения точки А(А₁, А₃)

1. а) Для построения А₁ через точку А₂(задана видимой) проводят параллель, замеряют радиус – R₂(от оси до очерка), строят горизонтальную проекцию этой параллели, проводят линию связи из точки А₂ Þ А₁.

б) Определяют видимость А₁ - невидима, т.к. точка А(А₂) на расположена ниже экватора ( на П₂ - в незаштрихованной зоне).

2. а) Для построения А₃ из точки А₂ проводят линию связи на П₃, на П₁ замеряют расстояние от фронтального меридиана (в₁)- Dу (параллельно оси У), переносят на П₃, откладывая от проекции фронтального меридиана (в₃) по линии связи (параллельно оси У) Þ А₃

б) Определяют видимость А₃ - видима, т.к. точка А(А₁) на П₁ расположена перед профильным меридианом (на П₁ в заштрихованной зоне) (рис.2-83).

Пример: F(i, l), а(а₂) Ì F, а₁, а₃ = ? (рис. 2-84)

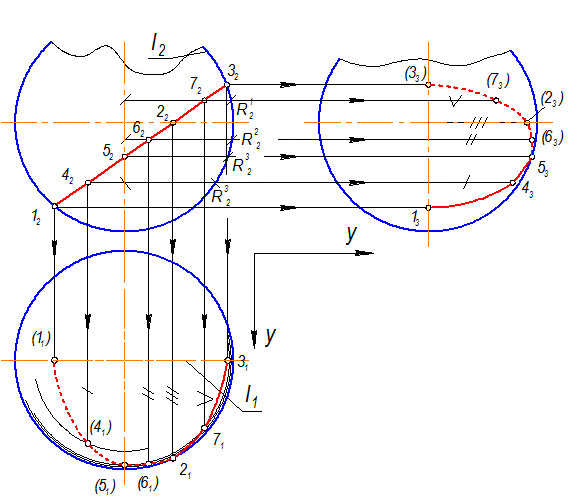
Рис. 2-84

1. Сначала отмечают особые точки (рис. 2-84):

Точка 2₂ Þ 2₁, 2₃ - по принадлежности экватору

Точки 1₂ Þ 1₁, 1₃ и 3₂ Þ 3₁, 3₃ - по принадлежности главному меридиану

Точка 5₂ Þ 5₁, 5₃ по принадлежности профильному меридиану

2. Промежуточные: 4, 6, 7 находят с помощью параллелей, радиусы которых замеряют от оси до очерка на П₂. Профильные проекции точек находят см. (рис. 2-83) Þ А₃.

<151617 18 19 20 21 >

Дата добавления: 2016-05-31; просмотров: 1643;