Энтропия. Второй закон термодинамики
Самопроизвольные процессы.В природе физические и химические превращения совершаются в определенном направлении. Так, два тела, находящиеся при разных температурах, вступают в контакт, тепловая энергия передается от более теплого тела к более холодному до тех пор, пока температура этих двух тел не сравняется. При погружении цинковой пластинки в соляную кислоту образуется ZnCl2 и H2. Все эти превращения являются самопроизвольными (спонтанными). Самопроизвольный процесс не может протекать в обратном направлении так же самопроизвольно, как в прямом.
В химии важно знать критерии, позволяющие предвидеть, может ли химическая реакция происходить самопроизвольно, и если может, то уметь определить количества образовавшихся продуктов. Первый закон термодинамики такого критерия не дает. Тепловой эффект реакции не определяет направления процесса. Самопроизвольно могут протекать как экзотермические, так и эндотермические реакции. Так, например, самопроизвольно идет процесс растворения нитрата аммония NH4NO3 (к) в воде, хотя тепловой эффект этого процесса положителен: 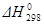 > 0 (процесс эндотермический); тоже самое можно сказать и о растворении гипосульфита натрия в воде. А в другом примере невозможно осуществить при Т = 298 К и p = 101 кПа (1 атм) синтез н. гептана C7H16 (ж), несмотря на то, что стандартная теплота его образования отрицательна:
> 0 (процесс эндотермический); тоже самое можно сказать и о растворении гипосульфита натрия в воде. А в другом примере невозможно осуществить при Т = 298 К и p = 101 кПа (1 атм) синтез н. гептана C7H16 (ж), несмотря на то, что стандартная теплота его образования отрицательна: 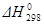 < 0 (процесс экзотермический).
< 0 (процесс экзотермический).
Таким образом, разность энтальпий реакции еще не определяет возможности ее протекания в данных конкретных условиях.
Второй закон термодинамики. Критерий самопроизвольного протекания процесса в изолированных системах дает второй закон термодинамики.
Второй закон термодинамики дает возможность разделить все допускаемые первым законом процессы на самопроизвольные и не самопроизвольные.
Второй закон термодинамики является постулатом, обоснованным большим опытом, накопленным человечеством. Он выражается разными эквивалентными формулировками:
1. Теплота не может переходить сама собой от менее нагретого тела к более нагретому - постулат Клаузиуса (1850 г). Утверждается, что процесс теплопроводности необратим.
2. Быстро или медленно всякая система стремится к состоянию истинного равновесия.
3. Невозможен периодический процесс, единственным результатом которого является превращение теплоты в работу - формулировка Кельвина - Планк.
4. Теплота может переходить в работу только при наличии разности температур и не целиком, а с определенным термическим коэффициентом полезного действия:
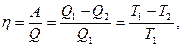
где η - термический коэффициент полезного действия; A – работа, полученная системой за счет перехода тепла от тела с высокой температурой (T1) к телу с низкой температурой (T2); Q1 – теплота, взятая у тела нагретого с температурой T1; Q2 – теплота, отданная холодному телу с температурой T2. Т.е. любые процессы протекают под действием разности потенциалов, каковой для тепловых процессов является разность температур, для электрических разность потенциалов, для механических - разность высот и т.д. Общим является сравнительно низкий коэффициент полезного действия. Значение к. п. д. обращается в единицу, если T2 → 0, но абсолютный нуль недостижим (третье начало термодинамики), следовательно, всю энергию нагретого тела при T1 в работу превратить нельзя. Т.е. при совершении работы часть общей энергии системы остается неиспользованной.
Понятие об энтропии.Исследуя выражение к.п.д. тепловой машины Клаузиус ввел новую термодинамическую функцию, которую назвал энтропией – S.
Работа идеальной тепловой машины (цикл Карно) подробно рассматривается в курсе физики.
Из математического выражения второго закона термодинамики следует:
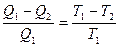 или
или 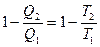
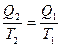 или
или 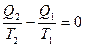
В дифференциальной форме:
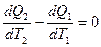
Суммируя изменения по всему циклу тепловой машины, получаем выражение 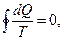 где dQ – приращение тепла, T – соответствующая температура;
где dQ – приращение тепла, T – соответствующая температура; 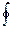 - интеграл по замкнутому контуру.
- интеграл по замкнутому контуру.
Подинтегральное выражение Клаузиус принял за приращение новой функции S – энтропии:
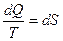 или
или 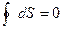
Энтропия представляет собой функцию параметров состояния системы (p, V, T) и может оценить направление процесса в системе, стремящейся к равновесию, т.к. для равновесного процесса ее изменение равно нулю; 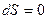 или
или 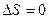 .
.
В случае необратимого превращения, т.е. спонтанного процесса, идущего при постоянной температуре, имеем 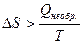
Если протекает процесс самопроизвольно, то изменение энтропии положительно: 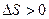
Для изолированных систем процессы, для которых изменение энтропии < 0, запрещены.
Если в качестве изолированной системы выбрать вселенную, то второе начало термодинамики можно сформулировать следующим образом:
Существует функция S, называемая энтропией, которая является такой функцией состояния, что
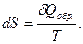
В случае обратимого процесса энтропия вселенной постоянна, а в случае необратимого процесса возрастает. Энтропия вселенной не может уменьшаться”.
Статистическая интерпретация энтропии.Для характеристики состояния некоторой массы вещества, являющейся совокупностью очень большого числа молекул можно указать параметры состояния системы и таким образом охарактеризовать макросостояние системы; но можно указать мгновенные координаты каждой молекулы (xi, yi, zi) и скорости перемещения по всем трем направлениям Vxi, Vyi, Vzi, т.е. охарактеризовать микросостояние системы. Каждому макросостоянию отвечает огромное число микросостояний. Число микросостояний, соответствующее макроскопическому состоянию определяется точными величинами параметров состояния и обозначается через W- термодинамическая вероятность состояния системы.
Термодинамическая вероятность состояния системы, состоящей всего из 10 молекул газа примерно 1000, а ведь только в 1 см3 газа содержится 2,7 ∙ 1019 молекул (н.у.). Поэтому в термодинамике используют не величину W, а ее логарифм lnW. Последнему можно придать размерность (Дж/К), умножив на константу Больцмана К:
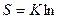 W, где
W, где 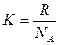 =1, 38 · 10-23 Дж/К,
=1, 38 · 10-23 Дж/К,
где NA – число Авогадро
Величину S называют энтропией системы. Энтропия – термодинамическая функция состояния системы.
Если изолированная система находится в макроскопическом состоянии 1, соответствующем W1 микроскопических состояний и если она может перейти в макроскопическое состояние 2, число микроскопических состояний которого W2, то система будет иметь тенденцию перейти в состояние 2 при условии, что W2 > W1
Система спонтанно стремится к состоянию, которому в микроскопическом масштабе соответствует наибольшее число возможностей реализации.
Например, при расширении идеального газа в пустоту конечное состояние (с большим объемом по сравнению с начальным состоянием) включает гораздо большее число микросостояний просто потому, что молекулы могут принимать большее число положений в пространстве.
Когда в изолированной системе происходит самопроизвольный процесс, число микроскопических состояний W возрастает; тоже самое можно сказать об энтропии системы. При возрастании числа микроскопических состояний W, связанных с макроскопическим состоянием системы, энтропия увеличивается.
Например, рассмотрим термодинамическое состояние 1 моль воды (18 г H2O) при стандартных условиях. Пусть W (ж) - термодинамическая вероятность состояния этой системы. При понижении температуры до 0 ºС вода замерзает, превращается в лед; при этом молекулы воды как бы закрепляются в узлах кристаллической решетки и термодинамическая вероятность состояния системы уменьшается; W (к) < W (ж). Следовательно, падает и энтропия системы: 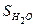 (к) <
(к) < 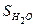 (ж). Наоборот при повышении температуры до 100º С вода закипает и превращается в пар; при этом термодинамическая вероятность состояния системы увеличивается: W (г) > W (ж), следовательно, растет и энтропия системы:
(ж). Наоборот при повышении температуры до 100º С вода закипает и превращается в пар; при этом термодинамическая вероятность состояния системы увеличивается: W (г) > W (ж), следовательно, растет и энтропия системы:
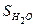 (г) >
(г) > 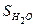 (ж).
(ж).
Энтропия, таким образом, является мерой неупорядоченности состояния системы. Действительно, единственному микроскопическому состоянию (W = 1) будет соответствовать полная упорядоченность и нулевая энтропия, т.е. известны положение, скорость, энергия каждой частицы, и все эти микроскопические характеристики будут оставаться постоянными во времени.
Второй закон термодинамики можно сформулировать следующим образом:
Изолированная система стремится достигнуть наиболее вероятного состояния, т.е. макроскопического состояния, соответствующего наибольшему числу микроскопических состояний.
В изолированных системах самопроизвольно идут только те процессы, которые сопровождаются ростом энтропии системы: Δ S > 0 (Δ S = S2 – S1).
Энтропия чистых веществ, существующих в виде идеальных кристаллов при температуре абсолютного нуля равна нулю. Это значит, что при абсолютном нуле достигается полная упорядоченность.
Дата добавления: 2016-12-09; просмотров: 4800;











