Циркуляция вектора магнитной индукции (закон полного тока). Следствие.

Магнитное поле в отличие от электростатического — непотенциальное поле: циркуляция вектора В магнитной индукции поля вдоль замкнутого контура не равна нулю и зависит от выбора контура. Такое поле в векторном анализе называют вихревым полем.

Рассмотрим в качестве примера магнитное поле замкнутого контура L произвольной формы, охватывающего бесконечно длинный прямолинейный проводник с током l, находящегося в вакууме (рис.12.8).

Линии магнитной индукции этого поля представляют собой окружности, плоскости которых перпендикулярны проводнику, а центры лежат на его оси (на рис. 12.8 эти линии изображены пунктиром). В точке А контура L вектор В магнитной индукции поля этого тока перпендикулярен радиусу-вектору .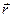

Из рисунка видно, что

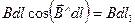
где 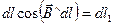— длина проекции вектора dl на направление вектора В. В то же время малый отрезок dl₁ касательной к окружности радиуса r можно заменить дугой окружности: 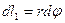, где dφ — центральный угол, под которым виден элемент dl контура L из центра окружности.

Тогда получаем, что циркуляция вектора индукции

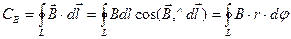
Во всех точках линии вектор магнитной индукции равен

,

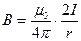интегрируя вдоль всего замкнутого контура, и учитывая, что угол изменяется от нуля до 2π, найдем циркуляцию

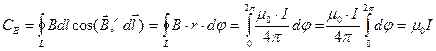
Из формулы можно сделать следующие выводы:

1. Магнитное поле прямолинейного тока – вихревое поле и не консервативно, так как в нем циркуляция вектора В вдоль линии магнитной индукции не равна нулю;

2. циркуляция вектора В магнитной индукции замкнутого контура, охватывающего поле прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции и равна произведению магнитной постоянной на силу тока.

Если магнитное поле образовано несколькими проводниками с током, то циркуляция результирующего поля

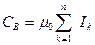
Данное выражение называется теоремой о полном токе.