АПРИОРНАЯ НЕОПРЕДЕЛЕННОСТЬ И ВОЗМОЖНЫЕ СПОСОБЫ НЕПОЛНОГО СТАТИСТИЧЕСКОГО ОПИСАНИЯ
Реализация байесова подхода в идеальном виде требует знания функциональной зависимости ожидаемой величины потерь - апостериорного риска - от решения u и значений х, описывающих данные наблюдения. В общем случае, для того чтобы приобрести это знание, необходимо достаточно полное статистическое описание данных наблюдения х и параметров состояния l, определяющих величину потерь. Его полнота должна быть достаточна для вычисления апостериорного риска при любом из возможных решений u. Без дополнительных ограничений чаще всего это возможно только тогда, когда известны распределения вероятности P(x | l) и р(l)для х и l.
На практике столь полное статистическое описание х и lвстречается относительно редко. Чаще всего задачи обработки информации и принятия решения сопровождаются большей или меньшей априорной неопределенностью, которая ограничивает полноту статистического описания. Обычная ситуация состоит в том, что нам известно о х и lнечто такое, что не дает возможности считать задачу синтеза совсем бессмысленной, но и не позволяет воспользоваться байесовым подходом в идеальном виде со всеми его преимуществами и возможностями. Распространенность подобных ситуаций и их большая практическая значимость делают особо важной разработку методов синтеза систем обработки информации и принятия решений в условиях априорной неопределенности.
Нужно подчеркнуть, что с момента своего зарождения классическая математическая статистика имела дело с задачами, в которых существенна априорная неопределенность. Такие важные разделы теории статистических решений, как теория проверки гипотез, особенно сложных, включающих мешающие параметры, разнообразные критерии согласия, теория оценок, использующая метод максимального правдоподобия и т. п., оперируют с задачами, связанными с весьма большой априорной неопределенностью и ограниченным статистическим описанием всех необходимых данных задачи.
Прежде чем переходить к их систематическому изложению рассмотрим основные возможные способы неполного статистического описания, соответствующие тем ограниченным сведениям о статистическом поведении данных наблюдения х и параметров состояния l, которые часто встречаются на практике. Надо заметить, что перечень рассматриваемых ниже характерных случаев и способов их описания ни в коей мере нельзя считать исчерпывающим. Он ограничивается, с одной стороны, широтой кругозора и симпатиями авторов, а с другой - возможностями решения задачи синтеза для той или иной степени априорной неопределенности.
3.1. ОТСУТСТВИЕ ИЛИ ОГРАНИЧЕННЫЕ СВЕДЕНИЯ ОБ АПРИОРНОМ
РАСПРЕДЕЛЕНИИ ПАРАМЕТРОВ
В практических задачах априорная трудность распространяется как на распределение вероятностей данных наблюдения P(x | l), так и на распределение р(l). При этом незнание либо весьма ограниченные сведения об априорном распределении р(l)особенно типичны. Рассмотрим поэтому сначала некоторые характерные ситуации, связанные с ограниченной априорной информацией о параметрах l.
1. Самой крайней ситуацией является случай, когда относительно l вообще ничего неизвестно, кроме, возможно, области L допустимых значений l, и той информации, которая содержится в данных наблюдения х, используемых непосредственно при принятии решения. Это означает, что априорное распределение р(l)вообще неизвестно и может быть любой неотрицательной функцией, подчиненной единственному условию нормировки  . Несмотря на такую крайность, задача синтеза оптимальной системы имеет смысл и соответствующие методы будут рассмотрены ниже.
. Несмотря на такую крайность, задача синтеза оптимальной системы имеет смысл и соответствующие методы будут рассмотрены ниже.
2. Близкая по смыслу ситуация, но существенно более выгодная с точки зрения качества синтезируемой системы (или качества принимаемого решения) имеет место, когда параметр lимеет векторный характер, но его компоненты связаны с помощью некоторых функциональных ограничений. Эти ограничения всегда можно привести к виду
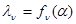 , (3.1.1)
, (3.1.1)
где 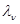 - n-я компонента l,
- n-я компонента l, 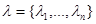 , а
, а 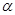 - некоторый векторный параметр меньшей чем п размерности,
- некоторый векторный параметр меньшей чем п размерности, 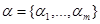 . Классическим примером подобного ограниченного описания является задача фильтрации - оценки функции времени (в данном случае рассматриваемой в дискретные моменты), заданной с точностью до некоторого числа неизвестных параметров
. Классическим примером подобного ограниченного описания является задача фильтрации - оценки функции времени (в данном случае рассматриваемой в дискретные моменты), заданной с точностью до некоторого числа неизвестных параметров 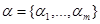 .
.
В этом примере 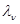 (n = 1, 2, …, n) - значения оцениваемой функции,
(n = 1, 2, …, n) - значения оцениваемой функции, 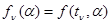 - ее функциональное описание в момент
- ее функциональное описание в момент 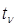 , зависящее от
, зависящее от 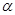 , параметры
, параметры 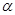 неизменны для всех интересующих нас значений n. Наиболее распространенным является полиномиальное описание, для которого
неизменны для всех интересующих нас значений n. Наиболее распространенным является полиномиальное описание, для которого
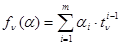 , (3.1.2)
, (3.1.2)
или более общее линейное описание относительно параметров 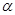
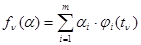 . (3.1.3)
. (3.1.3)
При наличии ограничений (3.1.1) функция потерь (по второму своему аргументу) g(u, l,, х) и функция правдоподобия P(x | l) зависят фактически только от 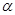 , и если о последних ничего неизвестно, то задача получается такой же, как в 1,за исключением понижения размерности с n до т. Последнее может быть очень существенным как с точки зрения техники решения задачи синтеза и получения окончательных результатов, так и качества полученного решения.
, и если о последних ничего неизвестно, то задача получается такой же, как в 1,за исключением понижения размерности с n до т. Последнее может быть очень существенным как с точки зрения техники решения задачи синтеза и получения окончательных результатов, так и качества полученного решения.
3. Во многих практических задачах, когда распределение P(l) не известно, можно считать заданными некоторые статистические характеристики l. Простейшей из них является математическое ожидание самого параметра l, которое во многих случаях можно предполагать заданным. Более подробное статистическое описание достигается, если заданы дисперсия l, моменты более высокого порядка и т. д. В общем случае подобные априорные сведения могут быть описаны путем задания математического ожидания некоторой многокомпонентной функции f(l). В итоге распределение вероятностей l получается не произвольным, а подчиненным следующим ограничениям:
 ;
; 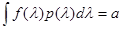 , (3.1.4)
, (3.1.4)
где f(l) — известная многокомпонентная векторная, матричная и т. д. функция l; а - заданная величина той же структуры.
Вид функции f(l) определяется структурой множества L и имеющимися сведениями. Например, если l - n-компонентный вектор 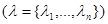 и заданы математические ожидания всех компонент, то
и заданы математические ожидания всех компонент, то 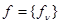
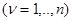 и
и 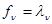 ,
, 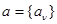
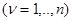 и
и 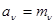 , где
, где 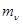 - заданное математическое ожидание
- заданное математическое ожидание 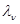 . Если дополнительно заданы дисперсии всех компонент
. Если дополнительно заданы дисперсии всех компонент 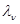 , то функция f имеет компоненты
, то функция f имеет компоненты 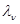 и (
и ( 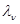 -
- 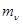 )2 (всего 2n компонент), а величина а соответственно
)2 (всего 2n компонент), а величина а соответственно 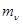 и
и 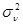 для
для 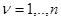 , где
, где 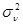 - заданная дисперсия
- заданная дисперсия 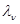 . Аналогичная картина имеет место и при задании других статистических характеристик.
. Аналогичная картина имеет место и при задании других статистических характеристик.
Как с практической, так и с теоретической точки зрения большое значение имеет специальный случай, когда задана корреляционная матрица 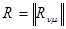 вектора l, (для простоты его математическое ожидание считается равным нулю), то есть
вектора l, (для простоты его математическое ожидание считается равным нулю), то есть
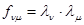 ;
; 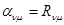 ;
; 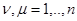 . (3.1.5)
. (3.1.5)
4. Следующим возможным способом ограниченного априорного описания n-мерного вектора параметров 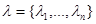 является задание распределений вероятности низшего порядка, например совокупности одномерных плотностей вероятности
является задание распределений вероятности низшего порядка, например совокупности одномерных плотностей вероятности 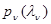 для всех или части n = 1, …, n, совокупности условных плотностей
для всех или части n = 1, …, n, совокупности условных плотностей 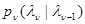 для n = 2, …, n, и т. д. Предположение о независимости
для n = 2, …, n, и т. д. Предположение о независимости 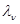 в первом случае или о марковском свойстве во втором совместно с заданием указанных характеристик дает полное статистическое описание
в первом случае или о марковском свойстве во втором совместно с заданием указанных характеристик дает полное статистическое описание  , но если даже такие предположения не имеют оснований, то все равно задание частных распределений вероятности дает богатую информацию для решения задач синтеза оптимальных систем.
, но если даже такие предположения не имеют оснований, то все равно задание частных распределений вероятности дает богатую информацию для решения задач синтеза оптимальных систем.
5. В п. 2 — 4 предполагалось задание некоторых аналитических, количественных свойств априорного распределения вероятности  , соответствующих наличию априорной неопределенности и дающих неполное статистическое описание. Пожалуй, большее значение имеют те ограниченные априорные сведения, которые относятся к качественному описанию свойств распределения вероятности параметров
, соответствующих наличию априорной неопределенности и дающих неполное статистическое описание. Пожалуй, большее значение имеют те ограниченные априорные сведения, которые относятся к качественному описанию свойств распределения вероятности параметров  . Например, весьма ценной является априорная информация о том, что различные компоненты
. Например, весьма ценной является априорная информация о том, что различные компоненты 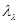 этой совокупности независимы (частные плотности
этой совокупности независимы (частные плотности 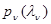 при этом неизвестны) или еще к тому же распределены одинаково, то есть
при этом неизвестны) или еще к тому же распределены одинаково, то есть
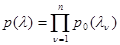 (3.1.6)
(3.1.6)
при полностью или частично неизвестной функции 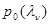 .
.
При решении задач синтеза в условиях априорной неопределенности равенство типа (3.1.6) может рассматриваться как гипотетическое и подлежащее проверке на соответствие с данными х, полученными при наблюдении. Особое значение в практических задачах имеет априорное предположение о том, что компоненты вектора 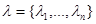 образуют марковский случайный процесс, то есть
образуют марковский случайный процесс, то есть
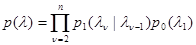 , (3.1.7)
, (3.1.7)
где переходная 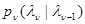 изначальная
изначальная 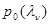 плотности вероятности могут быть полностью и частично неизвестны. Важность этого случая обусловлена его большой универсальностью, связанной с тем, что при надлежащем выборе размерности каждой из компонент
плотности вероятности могут быть полностью и частично неизвестны. Важность этого случая обусловлена его большой универсальностью, связанной с тем, что при надлежащем выборе размерности каждой из компонент 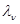 , которая, в свою очередь, может быть вектором, модель (3.1.7) удовлетворительно описывает большинство интересующих практику случаев.
, которая, в свою очередь, может быть вектором, модель (3.1.7) удовлетворительно описывает большинство интересующих практику случаев.
Общей чертой рассмотренных выше примеров является то, что в условиях априорной неопределенности вместо единственного распределения вероятности для параметров  , с плотностью
, с плотностью 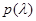 можно задать только класс таких распределений
можно задать только класс таких распределений 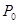 , к которому относятся все возможные в данной задаче распределения (
, к которому относятся все возможные в данной задаче распределения ( 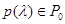 ). Такой класс является исходным описанием задачи и характеризует априорную неопределенность, тем большую, чем шире задаваемый класс. Так в «чисто» байесовом случае (
). Такой класс является исходным описанием задачи и характеризует априорную неопределенность, тем большую, чем шире задаваемый класс. Так в «чисто» байесовом случае ( 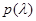 ) полностью известна) класс состоит всего из одного элемента, при полном отсутствии сведений об априорном описании параметров
) полностью известна) класс состоит всего из одного элемента, при полном отсутствии сведений об априорном описании параметров  , (случай 1)
, (случай 1) 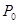 - класс всех возможных распределений вероятности. В случае 2 класс
- класс всех возможных распределений вероятности. В случае 2 класс 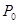 - это совокупность всех распределений в n-мерном пространстве, полностью сосредоточенных на гиперповерхностях, определяемых соотношениями (3.1.1), и приписывающих нулевую вероятностную меру остальной части пространства и т. д. Четкое определение класса возможных распределений
- это совокупность всех распределений в n-мерном пространстве, полностью сосредоточенных на гиперповерхностях, определяемых соотношениями (3.1.1), и приписывающих нулевую вероятностную меру остальной части пространства и т. д. Четкое определение класса возможных распределений 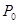 , соответствующего имеющимся априорным сведениям, имеет, как мы убедимся позднее, довольно существенное значение при решении задач синтеза в условиях априорной неопределенности.
, соответствующего имеющимся априорным сведениям, имеет, как мы убедимся позднее, довольно существенное значение при решении задач синтеза в условиях априорной неопределенности.
Дата добавления: 2018-05-10; просмотров: 2137;











