Исследование поведения заряженных частиц в магнитном поле.

Пусть частица, имеющая заряд q, движется в однородном магнитном поле перпендикулярно линиям магнитной индукции со скоростью v. На нее действует сила Лоренца

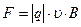
Так как поле однородно (В=const) и числовое значение скорости не меняется, то радиус кривизны остается постоянным. Поэтому частица будет двигаться по окружности.

Сила Лоренца является центростремительной

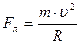
тогда

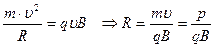
где р – импульс частицы.

Период вращения частицы в магнитном поле, т.е. время, за которое она совершает один полный оборот

.

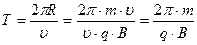Рассмотрим теперь общий случай движения заряженной частицы в однородном магнитном поле, когда ее скорость υ направлена под произвольным острым углом α к вектору индукции В поля (рис. 12.9).

Разложим вектор скорости v на две составляющие — параллельную вектору В (v_┴) и перпендикулярную ему (v_║):

v_║ = v· cos α ,

v_┴ = v ·sin α.

Скорость v_║ в магнитном поле не изменяется, т.е. 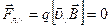. Следовательно, сила Лоренца не действует на частицу движущуюся вдоль силовой линии. По второму закону Ньютона

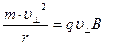
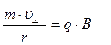
отсюда

.

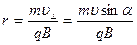Таким образом, частица одновремен­но участвует в двух движениях: она равномерно вращается со скоростью v_┴ по окружности радиуса r и движется поступательно c постоянной скоростью v_║ в направлении, перпендику­лярном плоскости вращения.

Поэтому тра­ектория заряженной частицы представляет собой винтовую линию, ось кото­рой совпадает с линией индукции магнит­ного поля (рис.12.10).

Расстояние между соседними витками называется шагом винтовой линии

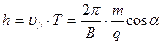
Устройства, применяемые для получения пучков заряженных частиц высокой энергии, называются ускорителями. По форме траектории ускоряемых частиц все ускорители можно разделить на две основные группы – линейные ускорители (траектория – прямая линия) и циклические (траектория – окружности или раскручивающиеся спирали) ускорители.

Одним из примеров таких циклических ускорителей является циклотрон. В основу его действия положена независимость периода обращения заряженной частицы в однородном магнитном поле от ее скорости.