Электрический заряд. Закон сохранения зарядов. Линейная, поверхностная и объемная плотности зарядов. Взаимодействие между зарядами.
Электростатика– это раздел электромагнетизма, который изучает электростатическое поле (т.е. поле, не меняющееся со временем).
Носителем электростатического поля является электрический заряд.
Заряды бывают положительный и отрицательный. Любой заряд можно представить как совокупность элементарных (удельных) зарядов.
Удельным отрицательным зарядом является заряд электрона е-=1,6·10-19 Кл.
Удельным положительным зарядом является позитрон, заряд которого е+=1,6·10-19 Кл.
Все тела делятся на положительно заряженные, отрицательно заряженные и нейтральные, в зависимости от соотношения положительных и отрицательных частиц, т.е.
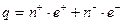 , ,
|
где n+ - количество элементарных положительных зарядов, n- - количество элементарных отрицательных зарядов.
q>0, если n+>n-
q<0, если n+<n-
q=0, если n+=n-
Экспериментально показано, что суммарный заряд электрически изолированной (замкнутой) системы не может изменяться, т.е.
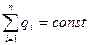
Это утверждение носит название закона сохранения электрического заряда. Система называется электрически изолированной (замкнутой или закрытой), если через ограничивающую ее поверхность не могут проникать заряженные частицы.
Рассмотрение электростатических взаимодействий заряженных тел начнем с простейшего случая взаимодействия точечных зарядов.
Точечным зарядом называется заряженное тело, размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми оно взаимодействует. Пробным зарядом называется положительный точечный заряд, который вносится в данное электромагнитное поле для измерения его характеристик. Этот заряд должен быть достаточно мал, чтобы не нарушать положение зарядов–источников измеряемого поля и тем самым, не искажать существующее поле. Таким образом, пробный заряд служит индикатором электромагнитного поля.
В случае протяженных зарядов, размерами которых пренебрегать нельзя, следует мысленно разбить их на достаточно малые элементы, каждый из которых может рассматриваться как точечный заряд.
В том случае, когда заряд распределен внутри макроскопического тела или некоторой области пространства, его пространственное расположение принято описывать с помощью (рис.10.1): объемной плотности заряда (r), 
поверхностной плотности заряда (s) и линейной плотности заряда (t).
Для линейного объекта (например, в случае заряженного стержня) вводят понятие линейной плотности заряда τ(рис.10.1, в),
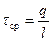 ,
где l –длина всего линейного объекта ,
где l –длина всего линейного объекта
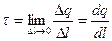 (10.1.1) (10.1.1)
|
где dq – заряд, приходящий на единицу длины dl.
Если объект двумерный (например, в случае заряженного проводника) вводят поверхностную плотность заряда(рис.10.1, б)
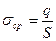 ,
, 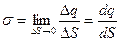 (10.1.2)
(10.1.2)
где dq – заряд, находящийся на элементе поверхности ds.
Для трехмерных объектов вводят объемные плотности заряда(рис.10.1,а)
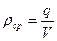 ,
, 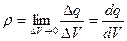 (10.1.3)
(10.1.3)
где dq – заряд малого элемента заряженного тела объемом dV.
Основной закон взаимодействия электрических зарядов был найден французским физиком Кулоном в 1785 году, экспериментальным путем с помощью крутильных весов.
По закону Кулона, сила электростатического взаимодействия двух точечных электрических зарядов, находящихся в вакууме прямо пропорциональна произведению этих зарядов (q1,q2), обратно пропорциональна квадрату расстояния между зарядами (r1,2) и направлена вдоль линии их соединяющей
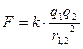 ,
,
где к – коэффициент пропорциональности (к>0).
 |
Если объекты одинаково заряжены, то они отталкиваются, а разноименные – притягиваются (рис.10.2).
Закон Кулона можно записать в векторной форме. Для этого введем обозначение единичного вектора 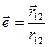 , имеющий направление от заряда q1 и q2.
, имеющий направление от заряда q1 и q2.
Соответственно сила взаимодействия зарядов
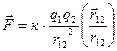 , ,
| (10.1.4) |
Или
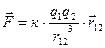 , ,
| (10.1.5) |
Для вакуума и воздуха коэффициент пропорциональности в законе Кулона 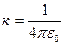 =9·109 Н·м2/Кл2, где
=9·109 Н·м2/Кл2, где 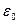 = 8,85·10-12 Ф/м – электрическая постоянная среды
= 8,85·10-12 Ф/м – электрическая постоянная среды
Безразмерная величина, характеризующая электрические свойства среды называется относительной диэлектрической проницаемостью среды 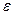 . Она не зависит от выбора системы отсчета и показывает во сколько раз сила взаимодействия между зарядами Q1 и Q2 в данной среде меньше, чем в вакууме. В вакууме диэлектрическая проницаемость среды равна единицы.
. Она не зависит от выбора системы отсчета и показывает во сколько раз сила взаимодействия между зарядами Q1 и Q2 в данной среде меньше, чем в вакууме. В вакууме диэлектрическая проницаемость среды равна единицы.
Опыт дает, что сила взаимодействия двух данных зарядов не изменяется, если вблизи них поместить еще какие-либо заряды. Поэтому электростатическая сила, с которой одно заряженное тело действует на другое, равно векторной сумме сил, приложенных ко всем точечным зарядам второго тела со стороны каждого точечного заряда первого тела.
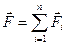
| (10.1.6) |
Эта формула позволяет, зная закон взаимодействия между точечными зарядами, вычислить силу взаимодействия между зарядами, сосредоточенными на телах конечных размеров.
 |
Например, найдем силу, взаимодействия заряда q и проволоки длиной l, расположенного на некотором расстоянии а (рис.10.3). Для этого разбиваем проволоку на бесконечно малые элементы, зарядом dq, чтобы их можно было считать точечными.
Тогда сила электрического взаимодействия можно определить по формуле (10.1.6), заменив знак суммы интегрированием.
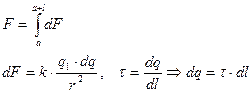
Дата добавления: 2016-12-09; просмотров: 2465;











