Теплоемкость твердых тел.
Тепловое движение в твердых телах заключается в колебаниях атомов относительно положений равновесия, расположенных в узлах кристаллической решетки. Атомы в решетке взаимодействуют, поэтому и колебания атомов являются не свободными, а связанными, однако по мере повышения температуры связь между атомами играет все меньшую роль в колебательных процессах и при достаточно высоких температурах можно принять, что колебания становятся свободными.
Рассмотрим по классической теории. На каждую степень свободы приходится энергия: 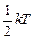 ; на i степеней свободы в одной молекуле:
; на i степеней свободы в одной молекуле: 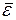 =
= 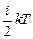 . Рассмотрим атомную решетку, для каждого атома в ней i=3:
. Рассмотрим атомную решетку, для каждого атома в ней i=3: 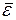 =
= 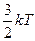 . Внутренняя энергия одного моля:
. Внутренняя энергия одного моля: 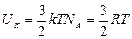 .
.
Однако атом, находящийся в узле кристаллической решетки, обладает не только кинетической энергией теплового движения, но и потенциальной энергией взаимодействия с соседними частицами, причем вклад этого вида сравним с кинетической: 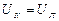
Внутренняя энергия одного моля одноатомного кристалла:
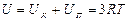 .
.
Объем твердого тела при нагревании изменяется слабо (b~10-5 1/К), то можно считать: 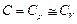 , тогда:
, тогда:
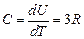 ,
,
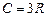 - закон Дюлонга и Пти
- закон Дюлонга и Пти
т.е. теплоемкость одного моля всех одноатомных кристаллов есть величина постоянная.
При комнатной температуре закон Дюлонга и Пти выполняется и примерно принимает значения около С=3R=25 Дж/(моль.К), то есть имеется соответствие с теорией. Но с классической точки зрения теплоемкость металлов должна быть значительно больше. В металлах имеются электроны проводимости, с классической точки зрения они обладают тремя степенями свободы. Если считать, что число их равно числу атомов, то электроны (как свободные частицы) должны внести в теплоемкость вклад Сэ=1,5 R, то есть увеличить ее на 50%. В действительности этого нет, и закон Дюлонга и Пти справедлив и для металлов.
Расхождение опытных и теоретических значений теплоемкостей, вычисленных на основе классической теории, объяснили, исходя из квантовой теории теплоемкости А. Эйнштейн и П. Дебай.
Дата добавления: 2016-12-09; просмотров: 1617;











