Экспериментальная проверка закона распределения Максвелла.

В равновесном состоянии параметры газа (давление, объем и температура) остаются неизменными, однако микросостояния – взаимное расположение молекул, их скорости – непрерывно изменяются. Из-за огромного количества молекул практически нельзя определить значения их скоростей в какой-либо момент, но возможно, считая скорость молекул непрерывной случайной величиной, указать распределение молекул по скоростям.

Теоретически задачу о распределении молекул идеального газа по скоростям поступательного движения решил Дж. К. Максвелл. Он показал, что число молекул, имеющих малые скорости и большие скорости относительно мало. Оказывается, что скорости большинства молекул лежат в окрестности некоторой средней скорости. С помощью теории вероятностей Дж. К. Максвеллу удалось вывести формулу для относительной частоты, с которой в газе при данной температуре встречаются молекулы со скоростями в определенном интервале значений.

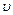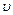Если N - общее число молекул газа, dN - число молекул, скорости которых заключены в интервале от до +d 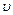, то закон распределения Максвелла запишется в виде:

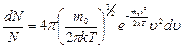
(6.6.1)

По определению плотности вероятности 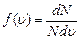, поэтому здесь

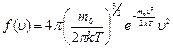
(6.6.2)

– функция распределения. Она указывает долю молекул dN/N, обладающих скоростями, лежащими в интервале dυ около значения скорости υ. Из этой формулы видно, что конкретный вид функции зависит от рода газа (m₀) и от параметров состояния (Т).

График функции распределения приведен на рис.6.5. Так как при возрастании скорости υ множитель 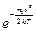уменьшается быстрее, и растет множитель υ², то функция 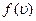, начинаясь от нуля, достигает максимума при υ_в и затем асимптотически стремится к нулю. Положение максимума характеризует наиболее часто встречающуюся скорость, которую называют наиболее вероятной скоростью u_в. Скорости, превышающие u_в, встречаются чаще, чем меньшие скорости. Кривая асимметрична относительно u_в.

Относительное число молекул, скорости которых находятся в интервале от u до u+du, находится как площадь заштрихованной полоски. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что f(u) удовлетворяет условию нормировки:

.

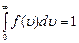(6.6.3)

Значение наиболее вероятной скорости υ_в находят, исследуя f(u) на экстремум:

.

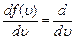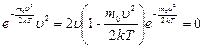(6.6.4)

Значения 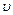=0 и 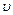=¥ соответствуют минимумам распределения (6.6.1), а значение v, при котором выражение в скобках равно нулю, и есть наиболее вероятная скорость: 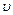_в= .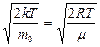

Из полученной формулы видно, что с повышением температуры газа максимум кривой распределения смещается в сторону больших скоростей (рис.6.6). Однако площадь, ограниченная кривой остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться, то есть наиболее вероятная скорость возрастает, а доля молекул, обладающих этой скоростью, уменьшается.

Если выразить скорости молекул не в обычных единицах, а в относительных, приняв за единицу скорости наиболее вероятную скорость молекул, то распределение Максвелла принимает вид:

,

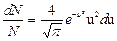(6.6.5)

где u= 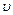/ 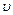_в – относительная скорость молекул.

Средняя скорость молекулы ` 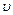(средняя арифметическая скорость) определяется из условия:

.

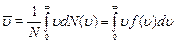Подставляя сюда f( 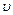) и интегрируя, получаем:

.

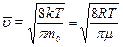(6.6.6)

Существует несколько способов проверки уравнения Максвелла. Наиболее убедительным оказался опыт О.Штерна (1920 г.).

Прибор состоял из двух коаксиальных цилиндров (рис.6.7). По оси прибора была натянута платиновая нить, покрытая серебром. При нагревании нити электрическим током с ее поверхности испарялись атомы серебра. Скорости испарившихся атомов соответствовали температуре нити. Внутренний цилиндр имел узкую продольную щель, через которую проходил наружу узкий пучок атомов, достигнув поверхности внешнего цилиндра, атомы серебра оседали на ней, образуя слой в виде узкой полоски.

Если привести прибор во вращение, след, оставляемый молекулярным пучком, сместится на некоторую величину DS, так как за время, пока атомы пролетают зазор между цилиндрами, прибор успевает повернуться на угол Dj:

;

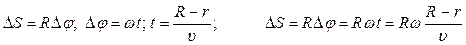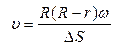
Измерив радиусы цилиндров R и r, смещение следа DS и скорость вращения прибора w, можно определить скорость атома. Вследствие распределения по скоростям атомы имеют различные скорости, и в результате смещенный слой будет размытым. Исследуя профиль следа, можно было составить примерное представление о распределении атомов серебра по скоростям. Он оказался в хорошем соответствии с видом максвелловского распределения.