Газовые законы. Уравнение Менделеева-Клапейрона.
Экспериментальное исследование свойств газов, проведенное в ХVII-XVIII вв. Р. Бойлем (1627-1691 гг.), Э. Мариоттом (1620-1684 гг.), Ж. Гей-Люссаком (1778-1850 гг.) и Ж. Шарлем привело к формулировке газовых законов:
1. Изотермический процесс - t=const
 |
Закон Бойля-Мариотта: для данной массы газа, при постоянной температуре, произведение давления газа на объем остается величиной постоянной, то есть при T = const и m = const (см. рис. 6.2):
| P×V = const | (6.5.1,а) |
или
| P1×V1 = P2×V2. | (6.5.1,б) |
2. Изобарный процесс - p=const.
Закон Гей - Люссака: для данной массы газа, при постоянном давлении, объем линейно возрастает с увеличением температуры, то есть при р = const и m = const (см. рис. 6.3):
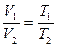
| (6.5.2,а) |
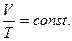
| (6.5.2,б) |
 |
или
3. Изохорический процесс - V=const.
Закон Шарля: для данной массы газа, при постоянном объеме, давление линейно возрастает с увеличением температуры, то есть при V = const и m = const (см. рис. 6.4):
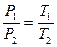
| (6.5.3,а) |
или
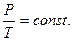
| (6.5.3,б) |
 |
Комбинируя выражения газовых законов, получим уравнение, связывающее р, V, Т (объединенный газовый закон):
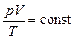 .
.
Постоянная в этом уравнении определяется экспериментально. Для 1 моль газа она оказалась равной R=8,31 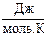 и была названа универсальной газовой постоянной.
и была названа универсальной газовой постоянной.
1 моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде массой 0,012 кг. Число молекул (структурных единиц) в 1 моле равно числу Авогадро: NA=6,02·1023моль-1. Для газовой постоянной R справедливо соотношение: R=k NA
Итак, для одного моля: 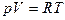 .
.
Для произвольного количества газа n = m/m (уравнение Менделеева-Клапейрона): 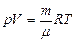 ,
,
где m - молярная масса газа.
Установим связь между уравнение кинетической теории газов и уравнением Менделеева-Клапейрона. 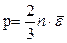
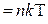 ,
, 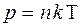 .
.
Так как n=N/V, то 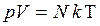 . Для количества вещества справедливо соотношение
. Для количества вещества справедливо соотношение 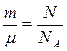 , а для постоянной Больцмана – k = R/NA, поэтому последнее уравнение можно записать в виде:
, а для постоянной Больцмана – k = R/NA, поэтому последнее уравнение можно записать в виде:
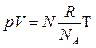 или
или 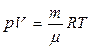 .
.
Дата добавления: 2016-12-09; просмотров: 1767;











