Молекул. Закон Дальтона.

При переходе к равновесию от одной части газа к другой передается энергия. Выравнивается не энергия всего газа как целого, а средняя кинетическая энергия, отнесенная к одной молекуле. Температура газа пропорциональна средней кинетической энергии его молекул: Т ~ 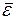. Средняя кинетическая энергия поступательного движения молекулы

= ,

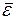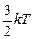(6.4.1)

где k - постоянная Больцмана, выражающая соотношение между единицей энергии и единицей температуры: k=1,38·10^-23 Дж/К.

Все молекулы при данной температуре Т имеют одну и ту же среднюю энергию независимо от их сорта. Из формулы (6.4.1) следует, что абсолютная температура является мерой средней кинетической энергии поступательного хаотического движения молекул. При Т=0 замирает тепловое движение, но остаются другие, нетепловые формы движения в веществе, например, движение электронов в атоме. Это движение нельзя прекратить, охлаждая вещество.

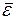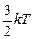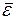
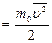Выразим теперь u_кв через абсолютную температуру Т. Приравнивая правые части в формулах = и получим u_кв= .

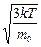Введем понятие универсальной газовой постоянной R, которая связана с постоянной Больцмана соотношением 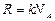, где N_A=6·10²³моль^-1 – число Авогадро (число молекул в одном моле вещества), и молярной массы m= N_am₀ –массы одного моля газа. Тогда среднюю квадратичную скорость поступательного движения молекул можно выразить формулой:

uкв= .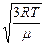

(6.4.2)

Подставляя в основное уравнение кинетической теории газов это выражение, получим, что давление идеального газа связано с температурой соотношением:

.

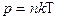(6.4.3)

Давление определяется только концентрацией (при постоянной температуре) и не зависит от сорта молекул.

Если имеем смесь нескольких газов, концентрация молекул которых n₁, n₂, ..., n_i и 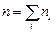, то

.

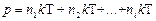Давления 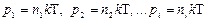называют парциальными давлениями. Например, р₁ – парциальное давление соответствует давлению, которое оказывал бы первый газ, входящий в состав смеси, если бы он занимал весь объем.

Согласно закону Дальтона в случае идеальных газов

.

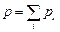(6.4.4)

Таким образом, давление, оказываемое на стенки сосуда смесью газов, равно сумме парциальных давлений отдельных компонентов смеси.