Основное уравнение кинетической теории газов.

Основным уравнением кинетической теории газов называется соотношение, связывающее давление (величину, измеряемую на опыте) со скоростью или кинетической энергией молекулы газа.

Рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа очень мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда элементарную площадку Ds (cм. рис.6.1) и вычислим давление, оказываемое на эту площадку. 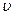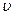При каждом соударении, молекула, движущаяся перпендикулярно площадке, передает ей импульс т₀ –(–m₀ ) = 2т₀ 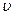, где т₀ – масса молекулы, υ – ее скорость. За время Dt площадки Ds достигнут только те молекулы, которые заключены в объеме цилиндра с основанием Ds и высотой 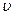Dt. Число этих молекул равно

N=nDs 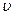Dt,

где п – концентрация молекул. Но необходимо учитывать, что реально молекулы движутся к площадке под разными углами и имеют различные скорости.

Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина из них (1/6) движется вдоль данного направления в одну сторону, половина — в противоположную.

Тогда число ударов молекул, движущихся в заданном направлении, о площадку Ds будет: .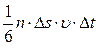

При столкновении с площадкой эти молекулы передадут ей импульс:

.

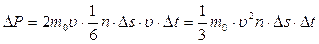Тогда давление газа на стенку сосуда:

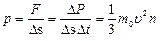
(6.3.1)

Если газ и объеме V содержит N молекул, движущихся со скоростями 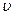₁, 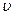₂., то учитывают среднюю квадратичную скорость

,

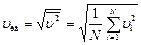(6.3.2)

характеризующую всю совокупность молекул газа. Уравнение (6.3.1) с учетом (6.3.2) примет вид

.

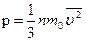(6.3.3)

Данное выражение называется основным уравнением молекулярно-кинетической теории идеальных газов. Это уравнение как раз и устанавливает связь между давлением и скоростью, вернее среднеквадратичной скоростью.

Введем среднюю кинетическую энергию хаотического поступательного движения одной молекулы 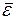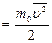. Тогда основное уравнение запишется как:

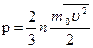
или

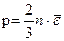
В данном уравнении давление связано со средней энергией поступательного движения молекул. Давление газа численно равно 2/3 средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.