Вязкость. Уравнение Ньютона.

Реальная жидкость отличается от идеальной тем, что она обладает внутренним трением, или вязкостью. Два соприкасающихся элемента жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый. Ньютон предположил, что величина этой силы (сила внутреннего трения) пропорциональна разности скоростей элементов жидкости.

Для нахождения количественных законов внутреннего трения рассмотрим две параллельные пластинки (рис. 5.8), между которыми находится слой жидкости.

Примем, что пластинки бесконечной длины L (т.е. L » h, где h – расстояние между пластинами). Нижняя пластина неподвижна, а верхняя движется со скоростью υ₀. Для поддержания равномерного движения необходимо приложить силу 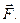Тогда на нижнюю пластинку АВ будет действовать сила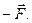

Из эксперимента установлено, что

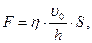
(5.5.1,а)

где S – площадь пластин, h - коэффициент вязкости. Если движется и пластинка АВ, то

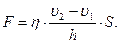
(5.5.1,б)

Если исследовать скорость частиц жидкости в разных слоях, то скорость является функцией координаты z, направленной вдоль линии наикратчайшего расстояния между пластинами, то есть υ = f(z). Частицы жидкости, соприкасающиеся с пластинами, имеют скорости, равные скорости пластин. Положим, что 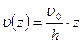.Тогда 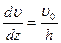и

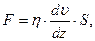
(5.5.2)

где величина 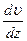(градиент скорости) показывает, как быстро изменяется скорость в направлении оси OZ. Коэффициент вязкости h определяется только свойствами жидкости, и в системе СИ измеряется единицей, равной 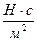. Уравнение (5.5.2.) называется уравнением Ньютона, поэтому жидкости, в которых внутреннее трение подобным образом зависит от изменения скорости, называются жидкостями с линейной вязкостью, или ньютоновскими жидкостями.