Применительно к двухмерной модели лопаточной машины

В процессе проектирования ЛМ часто возникает необходимость определения усилий, действующих со стороны потока на лопатки (или наоборот). Подобные задачи формулируются следующим образом.

Известны массовый расход через решётку элементарной ступени ЛМ, а также кинематика потока на входе в решётку и на выходе из неё.

Требуется определить усилие 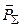, с которым поток действует на лопатку решётки элементарной ступени.

Для решения таких задач используется закон сохранения количества движения, который в теоретической механике записывается в виде

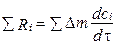(1.16)

и формулируется следующим образом: равнодействующая всех внешних и внутренних сил, действующих на тело массой Dm в произвольно выбранном направлении, равна секундному изменению количества движения этой массы в том же направлении.

Применим уравнение количества движения в форме (1.16) для решёток РК ОК и ОТ (рис. 1.16).

С этой целью в решётках ОК (рис. 1.16, а) и ОТ (рис. 1.16, б) выделим контрольные объёмы газа, ограниченные торцевыми сечениями 1-1^¢ и 2-2^¢, которые расположены соответственно перед решёткой и за ней. В этих сечениях поток считается равномерным и установившимся, кроме того, известна кинематика потока (c_{a i}, c_{u i} , a_i и т.д.).

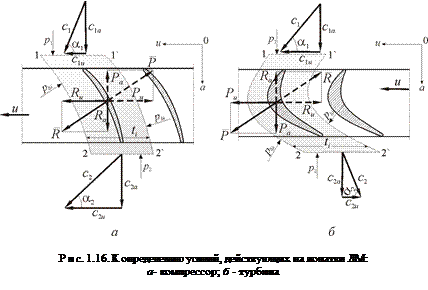
На расстоянии шага решётки t_i друг от друга расположены боковые поверхности 1-2 и 1^¢-2^¢. Они представляют собой конгруэнтные линии, в результате осевые и окружные проекции усилий от боковых давлений p_i равны нулю.

Внешними по отношению к выделенному объёму газа являются силы, создаваемые давлениями p₁ и p₂ по торцевым поверхностям 1-1^¢ и 2-2^¢. Силы R_a и R_u, действующие на газ со стороны лопаток, являются внутренними. Искомые силы (силы, действующие со стороны газа на лопатки) P_a и P_u по величине будут равны силам R_a и R_u соответственно, но противоположно направлены.

Найдем эти силы для компрессорной решётки. Учитывая положительные направления системы координат (см. рис.1.16, а), для силы R_u получим:

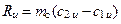, (1.17)

где m_c- секундный массовый расход, который можно определить из выражения m_c = r_i×c_ai×t_i×h_{л i} (здесь t_i и h_{л i} - соответственно шаг и высота решётки элементарной ступени ОК).

Тогда

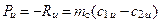. (1.18)

Сила P_u оказывает тормозящее воздействие на лопатки К в процессе сжатия, поэтому для его реализации к решётке РК следует подводить работу H_th.

Для осевой составляющей R_a силы 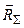можно получить следующее выражение:

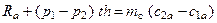
или, выделив R_a:

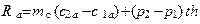. (1.19)

Сила R_a выполняет роль поршня, проталкивает газ в диффузорном межлопаточном канале вдоль оси “а”, когда к РК подводится работа H_th.

Осевая составляющая силы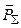

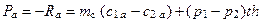. (1.20)

Как видно из рис. 1.16, а, сила P_a направлена в сторону полета ЛА и, следовательно, представляет собой одну из составляющих реактивной тяги двигателя.

Найдем силы P_u и P_a для решётки РК элементарной ступени ОТ. Используя выражение (1.16), в соответствии с обозначениями на рис.1.16, б получаем

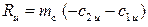. (1.21)

Соответственно для силы R_a:

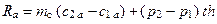. (1.22)

В результате значения усилий P_u и P_a могут быть найдены из выражений:

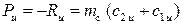. (1.23)

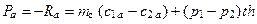. (1.24)

Направление силы P_u совпадает с направлением вращения решётки РК, поэтому она создает крутящий момент на валу ступени (совершает работу на лопатках). Сила P_a направлена в сторону, противоположную полету ЛА, поэтому считается, что Т, в отличие от К, создает отрицательную составляющую силы тяги.

Уравнения (1.19)...(1.20), а также (1.23)...(1.24), позволяют вычислить силы P_u и P_a в элементарных ступенях ОК и ОТ. Для расчёта усилий P_u и P_a в целом лопаточном венце его последовательно разбивают на 6...8 элементарных ступеней. При этом для каждой элементарной ступени вычисляются P_{u i} и P_{a i}. Общие же для лопаточного венца усилия P_u и P_a определяются простым алгебраическим суммированием усилий P_{u i} и P_{a i} в элементарных ступенях.