Уравнение моментов количества движения применительно к двухмерной модели лопаточных машин

Для установления связи величины подводимой (или отводимой) в ЛМ работы с элементами кинематики потока в теоретической механике используется закон сохранения моментов количества движения, который записывается в виде

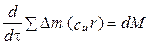(1.25)

и означает, что момент равнодействующей всех внешних и внутренних сил, действующих на некоторый объём относительно произвольно выбранной оси, равен секундному изменению момента количества движения выделенного объёма относительно той же оси.

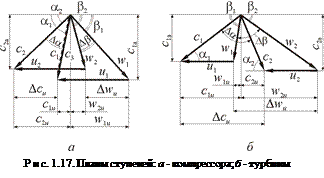
Рассмотрим планы скоростей элементарных ступеней ОК и ОТ (рис. 1.17) и применим к ним выражение (1.25). Рассматривая выражение (1.25) для элементарной ступени ОК и полагая, что массовый расход рабочего тела m_c = r_i×c_{a i}×h_{л i} t_i, получим

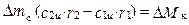. (1.26)

Поскольку в осевой ЛМ r₂ = r₁, то, умножая обе части уравнения (1.26) на w (частоту вращения ротора), имеем

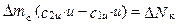. (1.27)

Если разделить DN_к на Dm_c, то получим H_th - удельную теоретическую работу. Тогда (1.27) примет вид:

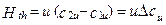(1.28)

или

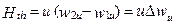, (1.29)

если u=const. Это означает, что удельная теоретическая работа, подводимая к рабочему телу в элементарной ступени ОК, численно равна произведению окружной скорости на разность проекций абсолютной (относительной) скорости на направление вращения.

Если внимательно посмотреть на план скоростей элементарной ступени ОК, то можно записать:

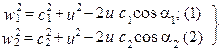
Вычитая почленно из (2) уравнение (1), с учётом (1.28) имеем:

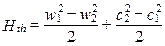, (1.30)

т.е. работа, подводимая в элементарной ступени ОК, тратится на изменение кинетической энергии в РК и НА.

Уравнение моментов количества движения для элементарной ступени ОТ запишется в виде

.

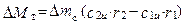В случае ОТ при принятой номенклатуре углов (см. рис. 1.17, б) и условии r₁ = r₂ получим

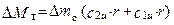. (1.31)

Умножив обе части выражения (1.31) на w, а также учитывая, что H_{т и} = DN_{т и} /Dm_c, имеем

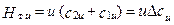(1.32)

или при условии u=const

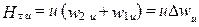. (1.33)

Записывая, по аналогии с элементарной ступенью ОК, вытекающие из плана скоростей ОТ соотношения, получаем:

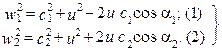
Складывая почленно (2) и (1), можно записать:

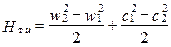, (1.34)

т.е. удельная теоретическая работа, совершаемая газом на лопатках РК ступени ОТ, получается за счёт изменения кинетической энергии в СА и РК.

Уравнения (1.16) и (1.25) применительно к осевым ЛМ позволяют сделать следующие выводы:

К и Т действительно являются обращёнными ЛМ. Это означает, что рабочий процесс в них аналогичен, но обращён, а описывающие его уравнения имеют одинаковую форму (см., например, (1.30) и (1.34)).

Существенно принципиальным различием является то, что в ступени ОК dp > 0 (идет процесс торможения потока), т.е. процесс диффузорный, а в элементарной ступени ОТ dp < 0 (идет процесс разгона потока), т.е. процесс конфузорный. Поскольку диффузорный процесс сопровождается большими потерями, чем конфузорный, угол раскрытия диффузора, характеризуемый Db, ограничивают, в результате Db_к << Db_т. При этом обычно в ступенях ОК Db_к = 20...30°, а в ступенях ОТ Db_т = 100...120°.

Из изложенного вывода следует, в частности, что H_{т u} >> H_th и, следовательно, число ступеней z_т существенно меньше z_к.

Рассмотренные в разделах 1.9...1.13 уравнения, описывающие рабочий процесс моделей осевых ЛМ, позволили существенно расширить представление о характере течения газа в элементах ЛМ и преобразованиях энергии в них. Однако представления о рабочем процессе в ЛМ не будут законченными, если не ввести в рассмотрение оценки эффективности процессов в К и Т.