К осевым лопаточным машинам

В термодинамике доказывается [20], что при переходе термодинамической системы из состояния i в состояние i + 1 изменение её полной энергии будет определяться выражением

DE_(i¸i+1) = ±DQ_вн ±DL_техн, (1.11)

где DQ_вн - количество тепла, подведенного (или отведенного) к системе; DL_техн - работа, выполненная системой во время цикла.

Применительно к осевым лопаточным машинам величину DE удобно подразделять на три составляющие:

изменение внутренней энергии – c_VDT, где DT - температурный интервал в процессе сжатия или расширения;

изменение потенциальной энергии сил давления - Dp/r;

изменение кинетической энергии - Dc²/2.

Для случая осевых ЛМ, когда К и Т выполняются неохлаждаемыми, выражение (1.11) принимает вид:

.

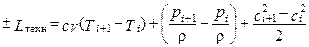В термодинамике сумму внутренней и потенциальной энергий сил давления называют энтальпией, т.е. c_VT_i + p_i /r_i = i_i. Тогда

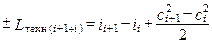. (1.12)

Очень часто, полагая i_i + c_i²/2 = i_i^*, выражение (1.12) записывают в виде

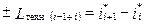. (1.13)

Выражения (1.12) и (1.13) применительно к осевым ЛМ носят название уравнения энергии в тепловой форме.

Нетрудно видеть, что уравнение энергии в форме (1.12) и (1.13) универсально: оно пригодно для описания как одномерных, так и двухмерных моделей рабочего процесса ЛМ. При этом под величинами p_i, T_i, c_i, r_i понимаются их некоторые средние значения, соответствующие рассматриваемой модели ЛМ.

Рассмотрим более подробно уравнение энергии применительно к К. Пусть в К к рабочему телу с расходом G_в подводится мощность N_к. Если поделить N_к на G_в, то получим удельную работу, сообщаемую в К 1 кг газа. В книгах эта величина обозначается H_к и носит название:

работа сжатия в К;

полная работа сжатия в К;

работа, затрачиваемая на сжатие;

внутренняя работа сжатия.

Определим размерность H_к:

.

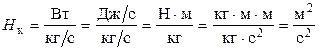Следовательно, величина H_к имеет размерность квадрата скорости.

Для одномерной модели ОК (1.12) примет вид:

,

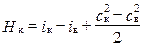т.е. удельная работа, подводимая в К, тратится на изменение теплосодержания и кинетической энергии.

В полных параметрах выражение (1.13) для К примет следующий вид:

H_к = i_к^* - i_в^*.

Если учесть, что i^* = c_pT^*, то из последнего выражения следует: при H_к >> 0

T_к^* >> T_в^*.

Запишем выражение (1.12) применительно к двухмерной модели ОК (см. рис. 1.11):

,

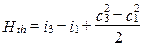откуда следует, что удельная теоретическая работа H_th, сообщаемая 1 кг газа в ступени, расходуется на изменение теплосодержания и кинетической энергии. В полных параметрах выражение (1.13) можно записать:

H_th = i₃^* - i₁^*,

здесь при H_th>> 0 - T₃^*>>T₁^*, т.е. температура торможения в ступени возрастает.

В силу универсальности уравнения (1.12) и (1.13) могут быть применены также и к отдельно взятым лопаточным венцам, при этом процесс можно рассматривать как в абсолютном, так и в относительном движении.

Рассмотрим, например, уравнение (1.13) применительно к решётке РК в относительном движении (см. рис. 1.11):

H_{РК (w)} = i^*_w2 - i^*_w1.

Так как H_{РК (w)} = 0, то i^*_w1 = i^*_w2 и, следовательно, T^*_w1 = T^*_w2, т.е. температура поверхности лопаток РК вдоль оси не изменяется.

Применительно к одномерной модели ОТ выражение (1.12) можно записать:

,

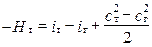здесь H_т взята со знаком (-), так как с точки зрения термодинамики [20] от газа отводится работа. В расчётной практике выгоднее иметь дело с положительными величинами, поэтому последнее выражение перепишем:

,

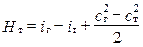откуда следует, что работа, совершаемая 1 кг газа в Т, осуществляется за счёт изменения теплосодержания и кинетической энергии. Используя выражение (1.13), получаем

H_т = i_г^* - i_т^*,

откуда следует, что при совершении газом работы температура его в Т уменьшается, т.е. T_т^* << T_г^*.

Аналогичные результаты можно получить, применив (1.12) и (1.13) к элементам ступени Т. Например, для СА можно записать (см. рис. 1.12):

H_СА = i₀^* - i₁^*,

откуда следует, что T₀^* = T₁^*, так как H_СА = 0.

Итак, уравнение энергии в тепловой форме позволяет связать величины H_i, T_i, T_i^* и c_i (или w_i). Однако, как в К, так и в Т происходит ещё и изменение p, поэтому возникает необходимость в такой записи уравнения энергии, где фигурировало бы давление p.