Уравнение энергии в механической форме

Для получения обобщенного уравнения энергии запишем в дифференциальной форме уравнение первого закона термодинамики и уравнение энергии в тепловой форме:

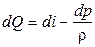; (1)

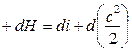. (2)

Сопоставляя (1) и (2), а также с учётом основных соотношений ЛМ dQ = dQ_тр и dQ_тр = dL_тр (L_r), получим

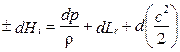(1.14)

или в интегральной форме:

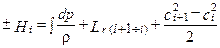(1.15)

Рассмотрим вначале применение обобщённого уравнения энергии (уравнения Бернулли) в форме (1.15) для К. Начнём с двухмерной модели, позволяющей получить более полное представление о характере процесса в ступени ОК. Запишем это уравнение (см. рис. 1.11) в виде

,

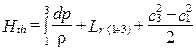откуда следует, что удельная работа, подводимая в ступени к 1 кг газа, тратится на повышение давления, на преодоление трения в ступени и на изменение кинетической энергии.

Последнее уравнение, в отличие от уравнения энергии в тепловой форме, содержит в качестве одного из членов величину L_{r (1¸3)}. Объясняется это тем, что в тепловой форме потери энергии фигурируют в виде тепла трения, которое остается в потоке (в виде энтальпии i = с_VT + p/r). В механической же форме потери присутствуют в виде работы по преодолению трения L_{r (i+1¸i)}, поэтому выражение (1.15) является более универсальным.

Для того, чтобы определить величину 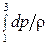, необходимо сделать предположение о характере процесса сжатия. Обычно в ступенях К принимают p×rⁿ = const, тогда

,

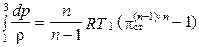где p_ст = p₃/p₁. Этот интеграл носит название политропической работы сжатия H_{п с}, поэтому уравнение (1.15) для К часто записывают в виде

.

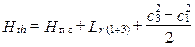Из последнего соотношения следует, что в случае, если c₃ = c₁ работа, подводимая к 1 кг газа в ступени, расходуется на политропическое сжатие и преодоление сил трения, что обусловливает целесообразность проектирования ступеней ОК, в которых c₃ = c₁. Обобщённое уравнение энергии в форме (1.15) можно записать и для отдельных лопаточных венцов, а также и в относительном движении. При этом, согласно принципу Даламбера, рабочий процесс во вращающемся РК ЛМ может быть заменен рабочим процессом в неподвижном венце, если характер обтекания решётки останется таким же, как и в относительном движении.

Соответственно можно записать:

.

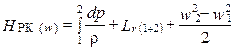Учитывая, что H_{РК (w)} = 0, получаем

,

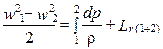т.е. изменение кинетической энергии в РК в относительном движении составляет сумму величин политропического сжатия и преодоления потерь энергии на трение.

На основании аналогичных рассуждений предлагаем студентам самостоятельно составить обобщенное уравнение энергии для РК и НА К, а затем проанализировать полученные выражения.

Запишем выражение (1.15) применительно к ступени ОТ:

.

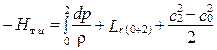Поменяв знак удельной теоретической работы, получим:

.

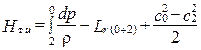Полагая процесс расширения политропическим p/rⁿ= const, для величины 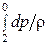получим:

,

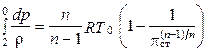где p_ст = p₀/p₂. Это выражение носит название политропической работы расширения H_{п р}.

Тогда (1.15) для Т можно записать:

.

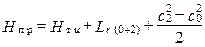Из этого соотношения следует, что политропическая работа расширения газа в ступени расходуется на совершение механической работы на валу, на преодоление сил трения вдоль оси ступени и на разгон потока, так как c₂> c₀.

Запишем уравнение энергии в механической форме для СА ОТ:

.

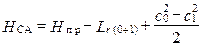Поскольку H_CA = 0, уравнение примет вид

,

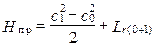что означает: работа расширения в СА ОТ идёт на разгон потока и преодоление сил трения.

Аналогичные выражения можно записать и для РК как в абсолютном, так и относительном движении. При этом будет получена дополнительная информация о рабочем процессе в ступени ОТ.

Закон сохранения энергии применительно к ЛМ помогает существенно расширить представление об их рабочем процессе. Однако выражения (1.12) и (1.15) не позволяют раскрыть механизм взаимодействия потока рабочего тела и лопаток, а также величин H_th (H_{т u}) с кинематикой потока в межлопаточных каналах. Для решения этих задач используются другие типы уравнений.