К одно- и двухмерным моделям лопаточных машин

Рассмотрим более подробно систему уравнений, описывающих модели ЛМ. Как отмечалось, в процессе проектирования ЛМ, часто приходится решать задачу по определению площади проходных сечений их проточной части. Задачи подобного типа формулируются следующим образом:

Известно, что по направлению оси “а” течёт расход рабочего тела G_i. Известны параметры рабочего тела на входе в ЛМ и на выходе из неё (p_i^* и T_i^*). Между сечениями на входе и выходе подводится (или отводится) некоторая мощность ±N_i.

Требуется определить потребные площади проточной части ЛМ в контрольных сечениях.

В таких задачах учитывается изменение параметров рабочего тела только вдоль оси “а”, следовательно, для их решения достаточно рассмотрения движения рабочего тела со скоростью c_a.

При решении подобных задач используется закон сохранения массы для элементарной струйки жидкости [9], который записывается в виде

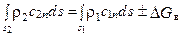(1.7)

и формулируется следующим образом: для равномерного и стационарного потока массовый расход жидкости через выходное сечение элементарной струйки равен массовому расходу через входное сечение с учётом стационарного вдува (+G_в) или отбора (-G_в).

Для одномерной модели ЛМ ± DG_в = 0, и выражение (1.7) примет вид

G_i = r₁ с_{1 a} F_{1 a} = r₂ с_{2 a} F_{2 a}, (1.8)

т.е. в любом сечении ЛМ в любой произвольно выбранный момент времени массовый расход воздуха не изменяется. А выражение (1.8) носит название уравнения неразрывности.

Простой анализ (1.8) показывает, что это уравнение позволяет:

связать термодинамические параметры (p_i^*, T_i^*) в любом сечении с величиной потребной площади;

установить изменение площади F_{a i} в зависимости от плотности тока r_i×c_{a i} (от характера процесса).

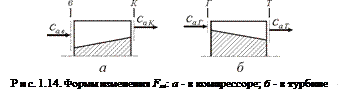
Последнее следствие показывает, например, что в К площадь должна уменьшаться от входа к выходу, т.е. F_{a к} < F_{a в} (рис. 1.14, а). Это вытекает из того факта, что в К r_к > r_в. Но тогда (при c_{a в} = c_{a к}) из (1.8) следует: F_{a к} < F_{a в}. В Т наблюдается обратная картина: r_т < r_г, и при c_г = c_т величина F_{a г} должна быть меньше F_{a т}.

Уравнение неразрывности часто используется и для двухмерных моделей ЛМ, например, при установлении связи между кинематическими параметрами потока и геометрическими параметрами элементарной ступени.

Такие задачи наиболее часто встречаются при проектировании решёток турбинных ступеней и формулируются следующим образом:

Известны параметры и кинематика потока рабочего тела в характерных сечениях решётки.

Требуется определить геометрические параметры решётки в тех же контрольных сечениях, которые обеспечивали бы заданное изменение кинематики и параметров потока.

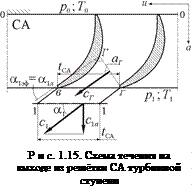На рис. 1.15 приведена схема течения потока на выходе из решётки СА турбинной ступени. Если известны параметры на входе в решётку СА (p₀, T₀) и на выходе из неё (p₁, T₁), то легко, с достаточной степенью точности, определить параметры потока и его кинематику в горле г-г межлопаточного канала. В этом сечении скорость потока c_г направлена к нему по нормали, следовательно, расход G_г = r_г с_г F_г, где F_г = a_г h_л. По отношению к выходному фронту решётки в-г скорость c_г направлена под углом a_{1 эф}, который определяется величиной a_г/t_СА (см. рис. 1.15). Этот угол называется эффективным и зависит только от геометрических параметров решётки СА на выходе.

В результате воздействия на поток стенки косого среза (участок г-в) в сечении 1-1 на входе в РК он имеет угол a₁, который отличается от a_{1 эф}. Установим связь между ними, применив уравнение неразрывности и полагая, что окружная протяженность контрольного сечения 1-1 также равна t_СА.

Для контрольных сечений г-г и 1-1 уравнение неразрывности примет вид

r_г с_г a_г h_л = r₁ с₁ t_СА h_л sina₁,

откуда

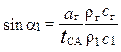. (1.9)

Учитывая, что (a_г/t_СА) = sina_{1 эф}, получаем

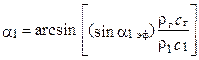. (1.10)

Выражение (1.10) определяет искомую связь величин a₁ и a_{1 эф}, которая, как видно, зависит не только от геометрических параметров решётки СА, но и от режима течения рабочего тела на участке косого среза.

Мы рассмотрели применение закона сохранения массы для ЛМ в виде уравнения неразрывности и установили его возможности для практики их газодинамического проектирования. Однако уравнение неразрывности не позволяет установить связь параметров потока с величиной подводимой (или отводимой) работы, в этом его ограниченность.