Изображение термодинамических процессов

в лопаточных машинах в p-V-диаграмме

ЛМ является не только механическим устройством, в котором к потоку рабочего тела подводится (либо отводится) работа. Процесс отвода (или подвода) работы сопровождается, как это следует из разделов 1.9...1.13, одновременным изменением p_i и T_i, что однозначно определяет ЛМ и как тепловую машину.

В этой связи возникает необходимость введения в рассмотрение некоторых оценок эффективности ЛМ как тепловых машин. Как известно из термодинамики [20], для определения важнейших энергетических параметров процессов в ЛМ - работ сжатия и расширения, гидравлических потерь и т.д. - используются термодинамические диаграммы.

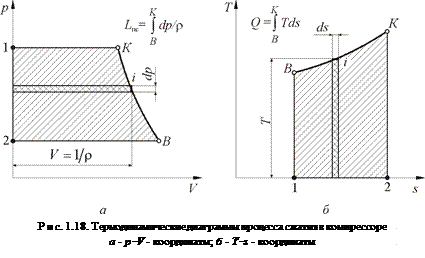
Вспомним основные свойства термодинамических диаграмм в p-V и T-s- координатах. На рис. 1.18 приведены термодинамические диаграммы процесса сжатия в К.

В p-V - координатах работа политропического сжатия ( 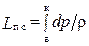) в компрессоре определяется площадью - 1-2-к-в, ограниченной изобарами p_к = const и p_в = const, а также политропой в-к, показатель которой n > k, где k - показатель изоэнтропы.

В T-s-координатах учитывается тепло Q, подводимое к потоку рабочего тела в термодинамическом процессе. В К к рабочему телу подводится только тепло от трения, поэтому площадь 1-в-к-2 соответствует теплу Q_тр, а, следовательно, и работе L_{r (в¸к)}.

Отсюда появляется возможность сравнения величин L_{п с} и L_r(в¸к) и, как следствие, получения оценок эффективности того или иного процесса в ЛМ.

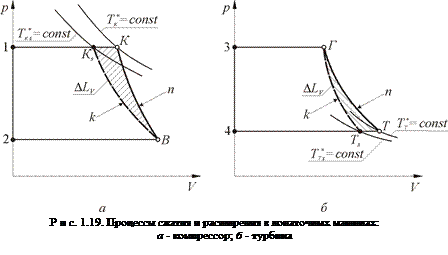
Рассмотрим процессы сжатия и расширения в лопаточных машинах в p-V-координатах (рис. 1.19).

Пусть кривая в-к_s соответствует изоэнтропическому сжатию в К. Величина работы определяется выражением [20]

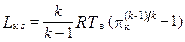, (1.35)

где p_к=p_к/p_в.

В реальном процессе выделяется тепло трения, которое вновь возвращается в поток, в результате чего T_{к s} < T_к, а следовательно, L_{п с}> L_кs. Разность L_{п с} - L_кs называется дополнительной объемной работой сжатия DL_V; она вызвана тем. что более нагретый газ сжать труднее. Таким образом, в p-V- координатах есть возможность сравнить L_кs и L_{п с}. Но в соответствии с (1.15) для введения оценок эффективности процесса надо знать L_к и L_{r (в¸к)}:

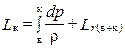(1.36)

(здесь принято, что c_в = с_к).

Выражение (1.36) запишем в виде составляющих:

L_к = L_{к s} + DL_V + L_{r (в¸к)}, (1.37)

откуда видно, что трение в проточной части К имеет двойное отрицательное воздействие. Действительно, для преодоления трения необходимо:

затратить работу L_{r (в¸к)}, в результате чего к потоку подводится Q_тр, пропорциональное L_{r (в¸к)}, и он подогревается;

совершить дополнительную работу DL_V, необходимость которой обусловлена сжатием более нагретого (по сравнению с изоэнтропическим процессом) потока.

Однако p-V- диаграмма процесса сжатия в К не позволяет оценить все составляющие в выражении (1.37), в этом заключается её ограниченность.

Рассмотрим теперь процесс расширения рабочего тела в Т в p-V- диаграмме (см. рис. 1.19, б). Пусть кривая г-T_s соответствует процессу изоэнтропического расширения. Величина L_тs определится из выражения [20]

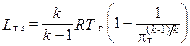, (1.38)

где p_т=p_г/p_т.

В реальном процессе расширения г-т из-за выделившегося тепла трения действительная температура T_т в конце процесса выше аналогичной температуры T_s и, следовательно, политропа г-т расположена правее изоэнтропы г-T_s. В результате L_{т п} больше L_тs на величину дополнительной работы объемного расширения DL_V, т.е. L_{т п} = L_тs + DL_V.

Из этих рассуждений вытекает парадоксальный вывод: в Т выгоднее реализовать несовершенный процесс расширения!!! Но это не так!

Из уравнения энергии, применительно к Т, следует:

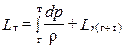(1.39)

(здесь принято c_г = с_т).

Выражение (1.39) можно переписать в виде

L_т = L_{т s} + DL_V - L_{r (г¸т)}. (1.40)

К сожалению, p-V-диаграмма не даёт представления о соотношениях величин DL_V и L_{r (г¸т)}, поэтому и возникает иллюзорный эффект относительно того, что в Т политропический процесс выгоднее изоэнтропического.

Из вышеизложенного следует, что для введения оценок эффективности процессов, происходящих в К и Т, следует рассмотреть их в других координатах, в которых все составляющие уравнений (1.37) и (1.40) можно было бы оценить количественно. К таким координатам относятся тепловые T-s- координаты.