Трёхмерная модель течения в лопаточной машине

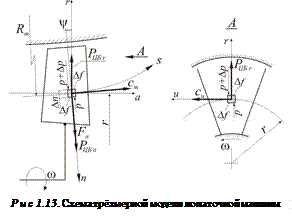Трехмерная модель течения рабочего тела в ЛМ используется в тех случаях, когда определяется меридиональная форма её проточной части, например, контуры обводов на втулке и на периферии лопаточного венца ступени ЛМ. На рис. 1.13 приведена схема трёхмерной модели ЛМ.

В трёхмерной модели проекция лопаточного венца ЛМ обычно рассматривается в меридиональной плоскости “m”. Пусть частица рабочего тела движется по линии тока s, при этом мгновенная скорость частицы определяется меридиональной составляющей скорости c_m, а мгновенный радиус кривизны линии тока равен R_m.

Для составления условия равновесия частицы на линии тока (это необходимо для определения формы линии тока и, следовательно, контуров обвода проточной части) введем координаты s и n: s - линия тока, n - мгновенная нормаль к линии тока в месте нахождения частицы рабочего тела. Декартову систему координат переместим в центр массы частицы рабочего тела (см. рис. 1.13) и предположим, что угол между нормалью n и радиусом r равен y.

Пусть протяжённость частицы рабочего тела вдоль нормали n равна Dn, а площадь её верхнего и нижнего оснований одинакова и равна Df. От оси ЛМ рассматриваемая частица отстоит на величину r (см. вид А на рис. 1.13), а окружная составляющая её скорости на этом радиусе равна c_u. На нижнее основание частицы действует гидродинамическое давление p, а на верхнее - p +Dp. Кроме того, со стороны лопатки на частицу действует сила .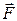

Поскольку частица движется по пространственной “винтовой линии”, вдоль нормали n действует центробежная сила 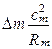, а вдоль радиуса r - .

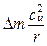Запишем условие равновесия частицы, находящейся на радиусе r:

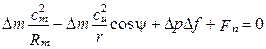. (1.3)

Учитывая, что Dm = r Dn Df, получаем

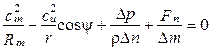. (1.4)

Уравнение (1.4) является уравнением движения рабочего тела в трёхмерной модели ЛМ.

Анализируя (1.4), можно решать несколько задач, связанных с определением линии тока или нахождением законов изменения параметров рабочего тела вдоль радиуса лопаточного венца.

Рассмотрим частный случай. Пусть линии тока s_i - прямые линии, параллельные оси ЛМ. Тогда

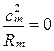; cosy = 1; Dn = Dr.

Кроме того, будем считать, что частица находится в межвенцовом зазоре (это не меняет физики модели, так как течение слоистое). Тогда F_n/D_m = 0.

С учётом этого выражение (1.4) примет вид

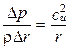, (1.5)

или в дифференциальной форме

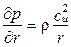. (1.6)

Мы получили уравнение (1.6), которое показывает изменение p вдоль r (следовательно, и других параметров) при условии слоистого течения и наличия закрутки c_u в ЛМ.

Рассмотренная модель течения называется квазитрёхмерной, так как составляющая c_r = 0 (течение слоистое), однако изменение других параметров – p, T и т.д. в данной схеме учитывается, поэтому она широко применяется в практике проектирования ЛМ.

Для анализа и расчёта рабочего процесса ЛМ, кроме моделей, требуются ещё и системы уравнений, которые описывают принятые схемы течения рабочего тела в проточной части.

Рассмотрим наиболее употребительные уравнения, применяющиеся в расчётной практике авиационных ЛМ.