Установившемся движении жидкости.

Как показывают опыты, потеря напора по длине может быть выражена через скоростной напор. В общем случае зависимость для потери напора, по длине записывается так: 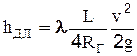(2-53), где L- длина потока, R_Г- гидравлический радиус. Для круглых труб (4R_Г=d) получим формулу Дарси-Вейсбаха:

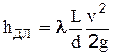(2-54)

где l- коэффициент гидравлического трения. В случае ламинарного режима движения была получена теоретическая формула для коэффициента гидравлического трения (2-50).

При турбулентном режиме движения жидкости коэффициент l находится по эмпирическим формулам. В общем случае коэффициент гидравлического трения зависит от числа Re и от шероховатости стенок русла D, т.е. l=f(Re,D).

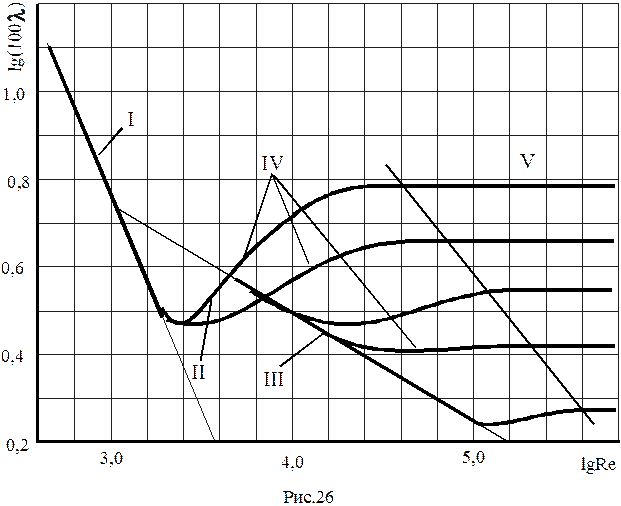
Вопросу влияния различных факторов на значение посвящено большое число экспериментальных и теоретических работ. Большой вклад в решение этого вопроса внес И. Никурадзе (1932 г.). Опыты проводились в трубах с искусственной однородной шероховатостью. В трубах с такой шероховатостью при различных расходах определялась потеря напора и по формуле (2-54) вычислялся коэффициент гидравлического трения и строился график l=f(Re). В области ламинарного режима (Re < 2300 или lgRe < 3,36) все опытные точки независимо от шероховатости уложились на одну прямую I . Следовательно, в этом случае l зависит только от критерия Рейнольдса Re и не зависит от шероховатости. При значениях Re от 2300 до 3000 l быстро возрастает с увеличением Re, оставаясь одинаковым для различных значений шероховатости. В области турбулентного режима (lg Re > 3,48 т.е. Re > 3000) начинает сказываться влияние шероховатости, при этом чем больше шероховатость, тем выше значение l для одних и тех же чисел Re. Для труб с большой шероховатостью l постепенно возрастает с увеличением Re, достигая некоторого постоянного значения. Для труб с малой шероховатостью опытные точки в некотором интервале располагаются вдоль наклонной прямой II (так называемая прямая Блазиуса для “гладких” труб). Отклонение от этой прямой наступает тем раньше, чем больше шероховатость. При этом l тоже стремится к некоторому определенному пределу (III). Это так называемая область вполне “шероховатых труб”, отвечающая квадратичному закону сопротивления (т.е. 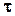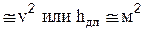). Таким образом всю область чисел на графике Никурадзе можно разделить на пять зон:

1 - ламинарный режим, l=f(Re);

2 - переходная из ламинарного в турбулентный режим, l=f(Re);

3 - область "гидравлически гладких" труб при турбулентном режиме, l=f(Re); 40 r/D <Re< 80 r/D;

4 - область шероховатых труб (доквадратичная область смешанного трения при турбулентном режиме, l=f(Re,D); 80 r/D <Re< 1000 r/D;

5 - область вполне шероховатых труб (квадратичная или автомодельная область) при турбулентном режиме, l=f(D); Re > 1000 r/D.

Основные закономерности, установленные Никурадзе, были в дальнейшем подтверждены и развиты рядом исследователей. В настоящее время, при определении коэффициента l, предпочтение отдают графику Г.А. Мурина. (или график ВТИ), который приводится практически во всех книгах по гидравлике. Во многих случаях предпочтительней пользоваться для определения не графиком, а расчетными зависимостями. Для зоны гладкого трения рекомендуют формулу Блазиуса: 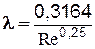или формулу Конакова: .

Рис.2.26.

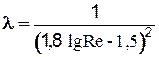Более универсальная формула Кольбрука-Уайта, применимая для всей области турбулентного течения: 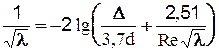. Известна формула А.Д. Альтшуля: 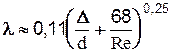. В квадратичной области вполне шероховатых труб - формула Б.Л.Шифринсона .

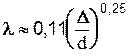Кроме формулы Дарси-Вейсбаха для определения потери напора по длине можно пользоваться целым рядом так называемых “специальных” формул (формулы Шези, Павловского и т.д.).