Истечение жидкости через отверстия и насадки

Истечение жидкости из отверстия - одна из основных задач гидравлики. Задача об истечении сводится к определению скорости истечения и расхода вытекающей жидкости. Наиболее просто и точно эта задача решается в случае, когда напор одинаков по всему поперечному сечению отверстия.

Рис.2.27.

Рассмотрим (рис.2.27.) случай истечения жидкости из горизонтального отверстия в дне сосуда. Пусть давление на свободной поверхности p₁, давление в среде, в которую происходит истечение p₂ (в общем случае эти давления отличны от атмосферного давления). Уровень жидкости в сосуде поддерживается постоянным, следовательно, движение установившееся. Для идеальной жидкости составим уравнение Бернулли для сечений 1-1 и 2-2. Площади сечений обозначим F и f. Плоскость сравнения 0-0 проведем через сечение 2-2.

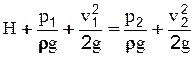
Из уравнения постоянства расхода 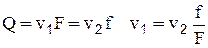, тогда

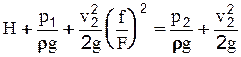
Отсюда найдем теоретическую скорость истечения:

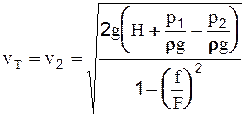(2-57)

Практически F>>f и отношением f/F можно пренебречь. В частном случае, когда p₁=p₂=p_АТМ (т.е. сосуд открыт и истечение происходит в атмосферу) получим формулу Торричелли:

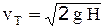(2-58)

Зная скорость истечения, определим теоретический расход жидкости:

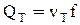(2-59)

При истечении реальной жидкости будут возникать потери напора в самом отверстии (т.е. потери напора могут быть отнесены к категории местных потерь). Особенностью этих потерь является то, что они обусловливаются торможением скорости вследствие трения жидкости о стенку и образованием пограничного слоя на поверхности струи, что приводит к неравномерности распределения скоростей. Поэтому действительная скорость истечения:

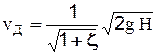(2-60)

здесь z - коэффициент местного сопротивления при истечении жидкости через отверстие.

Таким образом действительная скорость истечения будет меньше теоретической, т.к. некоторая часть энергии затрачивается на преодоление гидравлического сопротивления.

Отношение действительной скорости истечения к теоретической называется коэффициентом скорости j: .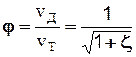

Струя жидкости при истечении претерпевает значительные изменения. Частицы жидкости в плоскости отверстия движутся по не параллельным траекториям, что обусловливает уменьшение площади поперечного сечения струи по выходе из отверстия. Например, при истечении из отверстия в тонкой стенке с острыми кромками струя жидкости испытывает сжатие и площадь ее сечения на некотором расстоянии от отверстия оказывается меньше площади отверстия. При этом в случае истечения через некруглые отверстия наблюдается также изменение формы струи (явление инверсии струи). В случае круглого отверстия струя со всех сторон подвергается одинаковому сжатию и в сжатом сечении также имеет форму круга (эллипса). Указанное явление характеризует коэффициент сжатия e - отношение площади сжатого сечения струи f_СЖ к площади сечения отверстия f : .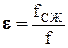

Поэтому уравнение Бернулли следует составлять для сжатого сечения, находящегося на некотором расстоянии от отверстия, где траектории струек можно считать параллельными, а давление - постоянным по всему сечению.

С учетом того, что v_Д = jv_T и f_СЖ =ef определим Q_Д = ejfv_T=mfv_T =mQ_T или с учетом (2-59):

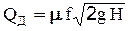(2-61)

где m=e j =Q_Д /Q_T - коэффициент расхода; показывает насколько действительный расход при истечении жидкости из отверстия уменьшается по сравнению с теоретическим в идеальном случае.

Обычно коэффициенты m, e определяют опытным путем, а j путем вычислений. Средние значения коэффициентов при истечении воды через донное отверстие в тонкой стенке: m=0,62; e=0,64; j=0,97.

Сжатие струи оказывается различным в зависимости от расположения отверстия, из которого происходит истечение жидкости, относительно боковых стенок сосуда. Сжатие называют совершенным, если отверстие находится на значительном расстоянии от стенок, и стенки не оказывают влияния на характер истечения. Опытами установлено, что совершенное сжатие наблюдается, когда расстояние от стенок до отверстия не меньше утроенной длины соответствующего размера отверстия. Если установленные условия не соблюдаются - сжатие называется несовершенным. Отверстием с полным сжатием, вытекающей из него струи жидкости, называется такое отверстие, в котором струя испытывает сжатие со всех сторон. Отверстием с неполным сжатием струи называется такое отверстие, когда вытекающая из него струя не имеет сжатия с одной или нескольких сторон.