Истечение при переменном напоре

Задача об истечении жидкости при переменном напоре обычно сводится к определению времени опорожнения или наполнения резервуара в зависимости от начального наполнения, формы, размеров сосуда и отверстия.

Рис.2.28.

В этом случае имеет место неустановившееся движение жидкости, что делает неприемлемым обычное уравнение Бернулли. Поэтому полное время истечения разделяют на бесконечно малые промежутки, в течение каждого из которых напор считают постоянным, а движение установившимся (т.е. независимым от времени).

Рассмотрим простейший пример истечения жидкости в атмосферу через донное отверстие площадью f из открытого вертикального цилиндрического сосуда, одинакового по всей высоте поперечного сечения F. Элементарный объем жидкости dV, прошедшей через отверстие за бесконечно малый промежуток времени dt определится dV=Qdt= 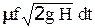, где H - глубина жидкости в сосуде для некоторого положения ее уровня, который можно приближенно считать постоянным. В действительности, однако, за это же время уровень жидкости в сосуде опустится на dH и объем жидкости в нем изменится на величину dW=-F dH. Вследствие неразрывности движения dV=dW, или

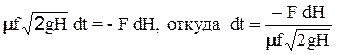(2-62)

Знак “-” т.к. высота H уменьшается и, следовательно, dH будет отрицательным.

Полное время t опорожнения определится в результате интегрирования выражения (2-62):

,

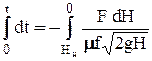где H_H - глубина жидкости до начала истечения.

Меняя пределы интегрирования и принимая m=const:

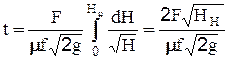(2-63)

Если нужно определить время, необходимое для понижения уровня жидкости в сосуде на некоторую величину от H₁ до H₂ исходят из того же уравнения (64) , интегрируя его в пределах от H₁ до H₂ , при этом:

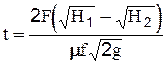(2-64)