Основное уравнение равномерного движения.

Рассмотрим (рис.2.19.) поток жидкости произвольной формы, имеющий по длине постоянное живое сечение S и наклоненное к горизонту под углом a. Выделим в потоке сечениями 1-1 и 2-2 отсек АВСD длиной L. Обозначим давления в центрах тяжести живых сечений 1-1 и 2-2 соответственно p₁ и p₂, геометрические высоты центров тяжести z₁ и z₂ (отметим, что ).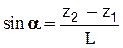

В условиях равномерного движения внешние силы, приложенные к жидкости, должны быть равны силам сопротивления, поэтому сумма проекций внешних сил на любую ось должна быть равна сумме проекций сил сопротивления на ту же ось (т.е. сумма проекций всех внешних сил, приложенных к указанному объему, на любую ось должна быть равна нулю). На выделенный объем действуют внешние силы: - силы давления F₁ и F₂ нормальные к этим сечениям:

Рис.2.19.

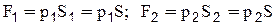(S₁ =S₂ =S. т.к. равномерное движение);

- силы гидродинамического давления p_n на боковую поверхность отсека АВСD со стороны окружающей его жидкости, направлены перпендикулярно к этой поверхности;

- сила тяжести (вес отсека), направлена по вертикали вниз: ;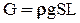

- силы сопротивления движению T, приложены вдоль поверхности стенок отсека. Обозначим через t силу трения, приходящуюся на единицу поверхности (т.е. касательные напряжения): T= t P L - эта сила направлена параллельно оси, но в сторону, обратную течению. Здесь P- смоченный периметр (2-20).

Составим уравнения проекций внешних сил на ось x-x (с учетом того, что p_n не дают проекции на эту ось).

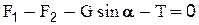, или

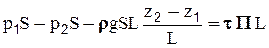
разделим все члены последнего уравнения на rgS:

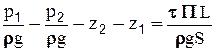, или

,

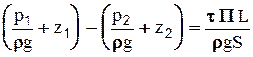так как кинетические энергии в сечениях 1-1 и 2-2 равны (равны площади сечений, значит, и скорости равны), то левая часть уравнения выражает потери напора на длине отсека (см.2-41):

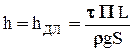(2-42)

основное уравнение равномерного движения.

Таким образом, сопротивления, возникающие при равномерном движении вязкой жидкости, прямо пропорциональны длине потока, смоченному периметру, напряжению силы трения на стенке и обратно пропорциональны площади живого сечения потока. Учтем, что 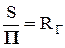(2-20), тогда уравнение (2-42) будет иметь следующий вид .

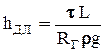Разделим на L: 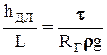. Т.к. 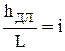(см. 2-39), получим:

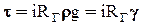(2-43)