Уравнение Бернулли для потока реальной жидкости.

Выведем уравнение Бернулли для установившегося потока вязкой (реальной) жидкости, состоящего из совокупности элементарных струек. Воспользуемся уравнением (2-33) для элементарной струйки. Т.к. мы предполагаем, что поток состоит из совокупности элементарных струек, то уравнение Бернулли для целого потока может быть получено путем суммирования (интегрирования) полных энергий всех элементарных струек, составляющих поток, и потерь энергии, в них происшедших.

Проинтегрировав уравнение (2-38) по живому сечению потока, получим уравнение Бернулли для потока реальной жидкости:

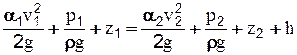(2-41)

Рис.2.18.

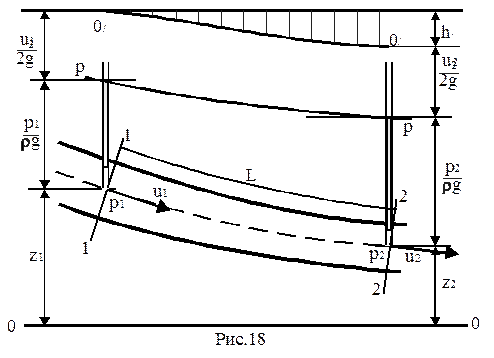
Т.е. мы установили, что уравнение Бернулли для целого потока вязкой жидкости по своему построению аналогично уравнению Бернулли для элемен-тарной струйки. Как бы увеличили элементарную струйку до размеров целого потока. Отметим важное отличие. Удельная кинетическая энергия или скоростной напор в уравнении Бернулли для потока реальной жидкости рассчитывается по средней скорости v движения жидкости.

Новым элементом здесь являются коэффициенты кинетической энергии (коэффициент Кориолиса) a, величина которых зависит от степени неравномерности распределения скоростей по живому сечению потока; они корректируют величину кинетической энергии при определении ее по средним скоростям v в соответствующих живых сечениях 1-1 и 2-2.Коэффициент a определяется опытным путем на основании специальных измерений скоростей в различных точках потока жидкости. Для ламинарного режима в круглых трубах a=2,0, а для турбулентного (развитого) a=1,05-1,1. Уравнение (2-41) является уравнением Бернулли для целого потока реальной жидкости. При этом сумма трех его членов - есть сумма трех удельных энергий целого потока вязкой жидкости в сечениях 1-1 и 2-2: 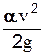- удельная кинетическая энергия потока; 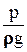- удельная потенциальная энергия давления; z - удельная энергия положения; h - потери энергии, происшедших при движении реальной (вязкой) жидкости от первого сечения ко второму.

Как уже указывалось, удельная энергия в гидравлике называется напором, поэтому уравнения Бернулли в геометрической интерпретации может быть представлено: H_Д1=H_Д2 + h, где H_Д1- полный напор потока в сечении 1-1; H_Д2- полный напор потока, в сечении 2-2; h- потери напора между сечениями 1-1 и 2-2.