В условиях установившегося движения.

Рис.2.20.

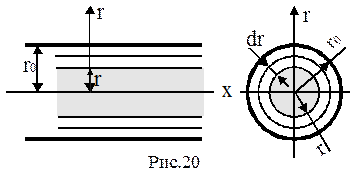
Рассмотрим наиболее интересный и важный для нас случай движения вязкой жидкости в напорном трубопроводе (рис.2.20.) круглого сечения радиусом r₀. Совместим ось x-х с осью трубы и наметим ось r по направлению измерения диаметра. Выделим внутри трубы цилиндрический столб движущейся жидкости радиусом r (заштрихован).

Для продольного касательного напряжения трения t по боковой поверхности жидкого столба можно записать два выражения:

-1 согласно закону Ньютона (2-6):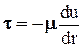

-2 cогласно уравнению равномерного движения (2-43): 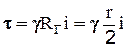(где ).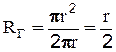

Решая совместно эти два уравнения относительно скорости u, получим:

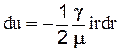. Интегрируя это уравнение получаем:

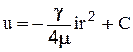. Постоянную интегрирования С находим из следующего условия: при r = r₀ u=0. Окончательно

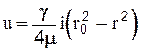(2-44)

Рис.2.21.

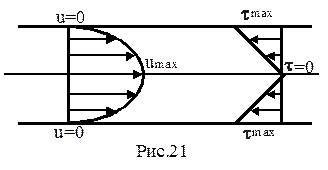
т.е. скорость изменяется по параболическому закону (рис.2.21). Причем при t=0 (в центре трубы) скорость максимальна .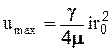

Или подставив это выражение в (2-44) получим закон Стокса:

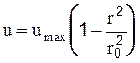(2-45)

Из выражения (2-6) следует, что величина напряжения сил трения изменяется по живому сечению трубы по линейному закону. При этом t_max при r=r₀ (у стенки) и t = 0 при r = 0(в центре трубы).

Определим расход жидкости, проходящей по трубе. Элементарный расход жидкости, проходящей через элементарную часть площади живого сечения в виде кольца толщиной dr, имеющего радиус r (рис.2.18.):

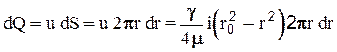
Интегрируя по всей площади живого сечения

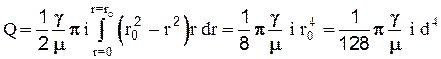(2-46)

- закон (формула) Гагена-Пуазейля.

Средняя скорость:

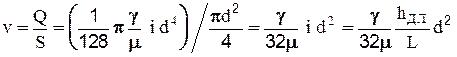(2-47)

Откуда:

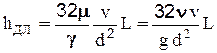(2-48)

Сопоставляя выражения (2-47) и (2-44) можно видеть, что в круглой трубе при ламинарном режиме движения средняя скорость v в два раза меньше максимальной, т.е. .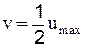

Из (2-48) видно, что потери напора по длине при ламинарном режиме движения пропорциональны первой степени скорости.

Установим выражение для гидравлического уклона. Разделим почленно уравнение (2-48) на L: 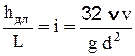, или, помножив и поделив на 2v, перепишем в виде 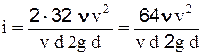, а т.к. 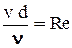, то 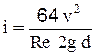(2-49)

Следовательно, гидравлический уклон при ламинарном режиме движения зависит от числа Re; выражение 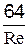обозначают 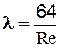(2-50) и называют коэффициентом гидравлического трения.

Окончательно формула для определения потери напора по длине может быть записаны:

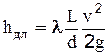(2-51)

-формула Дарси-Вейсбаха.