Уравнения динамики и статики. Линеаризация

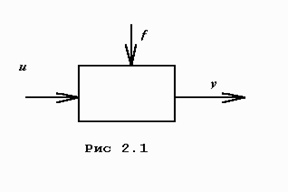
В общем случае звенья и системы описывают нелинейными дифференциальными уравнениями произвольного порядка. Под звеном понимается математическая модель элемента. Для примера рассмотрим звено (рис. 2.1), которое можно описать дифференциальным уравнением второго порядка

y=F ( , , )

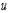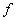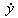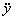(2.1)

где у — выходная величина, 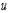и 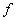— входные величины, 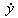и —первые производные по времени, 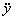— вторая производная по времени.

Уравнение (2.1), описывающее процессы в звене при произвольных входных воздействиях называют уравнением динамики. Пусть при постоянных входных величинах 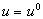и 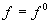процесс в звене с течением времени установится: выходная величина примет постоянное значение 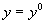. Тогда (2.1) примет вид

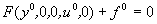
(2.2)

Это уравнение описывает статический или установившийся режим и его называют уравнением статики.

Статический режим можно описать графически с помощью статических характеристик. Статической характеристикой звена или элемента (а также системы) называют зависимость выходной величины от входной в статическом режиме. Статическую характеристику можно построить экспериментально, подавая на вход элемента постоянное воздействие и измеряя выходную величину после окончания переходного процесса, или расчетным путем, используя уравнение статики.

Если звено имеет несколько входов, то оно описывается с помощью семейства статических характеристик.