Алгоритм динамики – управляющий

Д00 УПР с комментариями

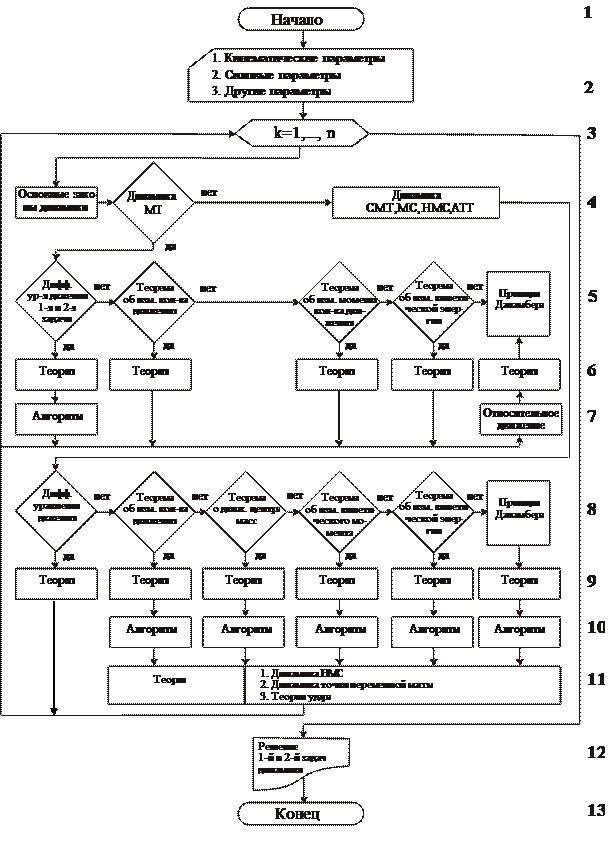
Комментарии

К.2. Вводятся для рассматриваемых объектов абстрактные понятия МТ, СМТ, МС, НМС и АТТ.

К.3. Определяется n – число МТ или n – число МТ, НМС, АТТ, входящих в СМТ.

К.4-6. Начинается изучение динамики с изучения движения МТ.

Определяются, используя четыре основных закона динамики, дифференциальные уравнения движения свободной и несвободной МТ, три теоремы динамики МТ и принцип Даламбера для МТ.

К.7. Рассматриваются алгоритм решения первой и второй задач динамики МТ и движение МТ в неинерциальной системе отсчета – относительное движение МТ.

К.8-9. Определяются, используя основные законы динамики и основные понятия динамики СМТ, дифференциальные уравнения движения СМТ, четыре теоремы динамики СМТ и принцип Даламбера для СМТ.

К.10. Рассматриваются алгоритмы решения задач с помощью четырех теорем динамики СМТ и принципа Даламбера для СМТ, приводятся комментарии к алгоритмам и примеры их использования.

К.11. Используются четыре теоремы динамики СМТ и принцип Даламбера для СМТ при рассмотрении динамики НМС, динамики МТ переменной массы и элементов теории удара.

К.12. В курсе теоретической механики раздел "Динамика" по существу связывает два предыдущих раздела – "Статика" и "Кинематика". Используются методы статики сложения сил и приведения различных систем сил к простейшему виду и методы кинематики в части, касающейся установления способов задания движения материальных объектов и определения их основных кинематических параметров движения.

В разделе "Динамика" решаются две основные задачи:

Первая задача (прямая) динамики заключается в том, чтобы, зная механическое движение определенного материального тела (его уравнения или кинематические параметры движения) представляя его в том или ином абстрактном образе (МТ, СМТ, МС, НМС, АТТ), найти силы, вызывающие это движение.

Вторая задача (обратная) заключается в том, чтобы, зная силы, приложенные к определенному материальному телу, представляя его в том или ином абстрактном образе (МТ, СМТ, МС, НМС, АТТ), найти механическое движение этого тела (его уравнения или кинематические параметры движения).

Классическая механика, основанная на законах Исаака Ньютона, не потеряла своего значения в современном мире, о чем говорил Альберт Эйнштейн: "Ньютон, прости меня! В твое время ты нашел тот единственный путь, который был пределом возможного для человека величайшего ума и творческой силы... Пусть никто не думает, что великое создание Ньютона может быть ниспровергнуто теорией относительности или какой-либо другой теорией. Ясные и широкие идеи Ньютона навечно сохранят свое значение фундамента, на котором построены наши современные физические представления".