Понятие о статистических параметрах
Параметры пассивных и активных электронных компонентов, из которых состоит РЭС, принимают случайные значения, то есть случайным образом отклоняются от номинальной величины. Однако эти случайные отклонения, вызванные неточностью изготовления компонентов при их производстве, лежат в определённых границах, называемых допусками. Так, например, если в партии резисторов с номинальным значением сопротивления R0=1200 Ом и допуском +/-10% замерить сопротивления всех резисторов, то окажется, что их значения не равны номинальному R0=1200 Ом, а больше или меньше его, но лежат в пределах от 0.9*1200=1080 Ом до 1.1*1200=1320 Ом.
Параметры РЭС зависят от случайных значений входящих в него электронных компонентов и, вследствие этого, также принимают случайные значения, о есть случайным образом отклоняются от своих номинальных величин. РЭС должно быть спроектировано таким образом, чтобы при заданных допусках на параметры компонентов случайные значения параметров самих устройств лежали в границах допусков на них. Допуски на параметры устройств определяют правильность функционирования и качество РЭС и задаются в соответствии с этими требованиями в документе, который называется “Технические условия” (ТУ). Для проверки выполнения требований ТУ к допускам на параметры РЭС обычно изготавливается партия устройств от нескольких десятков до нескольких сотен штук. Для каждого устройства из этой партии производятся измерения параметров. Любое РЭС из этой партии собрано из случайно выбранных электронных компонентов. Поэтому параметры каждого РЭС являются реализацией случайного процесса изготовления РЭС.
Изготовление и измерение партии стоит дорого и занимает много времени. Процесс изготовления и измерений РЭС является физической (натурной) реализацией статистических испытаний РЭС. В составе пакета программ схемотехнического моделирования есть режим статистических испытаний методом Монте-Карло, позволяющий исключить их физическую реализацию, используя математические модели.
Суть метода состоит в следующем. Для каждого электронного компонента РЭС значение параметра выбирается случайным образом, но в пределах допусков. Полученная таким образом модель РЭС имитирует изготовление РЭС в производстве. Для полученной модели производится расчет (анализ) её параметров по одной из программ анализа. Результаты анализа, то есть параметр устройства, запоминаются. Таким образом реализован один шаг метода Монте-Карло, то есть проведено одно статистическое испытание или, как говорят, одна выборка случайного процесса. Далее шаги повторяются, то есть опять для каждого компонента РЭС случайным образом выбирается значение параметра в пределах допусков на него. Вновь производится анализ и запоминание его результатов. Количество выборок - аналог количества устройств в партии задаётся при входе в режим статистических испытаний Монте-Карло. После выполнения заданного числа шагов n в памяти остаётся n значений параметра РЭС. Если наибольшее и наименьшее значения лежат в пределах, заданных в ТУ, то это означает, что в процессе производства данные устройства будут удовлетворять требованиям ТУ. Причём вероятность справедливости этого утверждения будет тем выше, чем большее количество выборок будет сделано.
Если окажется, что требования ТУ выполняются не для всех устройств, а только для части, то можно найти долю (в процентах) той части устройств, которая удовлетворяет требованиям. Это может быть сделано с помощью так называемой гистограммы распределения, которая автоматически строится при использовании режима Монте-Карло в пакете схемотехнического моделирования.
Поясним построение и использование гистограммы распределения на следующем примере. Пусть проводятся испытания усилителя, параметром которого является коэффициент усиления на частоте 1000 Гц в дБ, причём его значение в соответствии с ТУ должно лежать в пределах от 36 дБ до 46 дБ. Пусть по результатам статистических испытаний для 25 выборок (n = 25) получены следующие значения коэффициента усиления (табл. 3.1):
Полученные значения лежат в пределах от 31,8 дБ (испытание № 24) до 49,5 дБ (испытание № 9) и, следовательно, ряд усилителей не удовлетворяют требованиям ТУ.
Таблица 3.1.
| Номер выборки, i | ||||||||
| Ki, дБ | 35,2 | 41,6 | 33,6 | 39,1 | 44,2 | 37,4 | 41,8 | 41,4 |
| i | |||||||||
| Ki, дБ | 49,5 | 35,5 | 39,4 | 42,1 | 39,8 | 37,6 | 39,2 | 33,3 | 42,9 |
| i | ||||||||
| Ki, дБ | 46,1 | 42,7 | 39,3 | 36,9 | 44,5 | 41,9 | 31,8 | 41,2 |
Рассчитаем, какая часть усилителей (в %) удовлетворяют этим требованиям, для чего используем гистограмму распределения, которая строится следующим образом. Разделим весь диапазон полученных значений коэффициента усиления на 10 поддиапазонов:
1 поддиапазон – от 30,0 дБ до 32,0 дБ;
2 поддиапазон – от 32,0 дБ до 34,0 дБ;
3 поддиапазон – от 34,0 дБ до 36,0 дБ;
4 поддиапазон – от 36,0 дБ до 38,0 дБ;
5 поддиапазон – от 38,0 дБ до 40,0 дБ;
6 поддиапазон – от 40,0 дБ до 42,0 дБ;
7 поддиапазон – от 42,0 дБ до 44,0 дБ;
8 поддиапазон – от 44,0 дБ до 46,0 дБ;
9 поддиапазон – от 46,0 дБ до 48,0 дБ;
10 поддиапазон – от 48,0 дБ до 50,0 дБ.
Для каждого поддиапазона вычислим количество усилителей, коэффициент усиления которых лежит в пределах поддиапазона, и их долю (в %) от общего числа усилителей (n =25). Результаты вычислений занесены в табл. 3.2:
Таблица 3.2.
| № подди-апазона | ||||||||||
| Границы поддиапа-зона, дБ | 30-32 | 32-34 | 34-36 | 36-38 | 38-40 | 40-42 | 42-44 | 44-46 | 46-48 | 48-50 |
| Количество усилителей | ||||||||||
| Доля, % |
Построим график, по оси X которого отложим усиление (в дБ), а по оси Y – долю усилителей (в %). Полученная кривая (рис. 3.4) называется гистограммой распределения
 |
В соответствие с этой гистограммой для диапазона, указанного в ТУ (36 – 45 дБ) путём суммирования долей в % находим, что только 72 % изготавливаемых усилителей будут удовлетворять требованиям ТУ, а остальные являются браком. Причиной этого являются слишком большие допуски на параметры электронных компонентов. Следовательно, необходимо применить другие компоненты, имеющие меньшие значения допусков.
В режиме Монте-Карло помимо построения гистограммы распределения рассчитываются среднее значение Mean и среднеквадратическое значение Sigma исследуемого параметра РЭС. Среднее значение – это наиболее вероятное значение параметра РЭС в процессе изготовления, а среднеквадратическое значение - это наиболее вероятное отклонение от среднего значения, которое может принимать параметр устройства в процессе изготовления. Для рассмотренного ранее примера по данным табл. 3.1 получим:
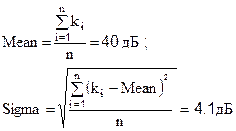
Зачем и как использовать значения Mean и Sigma ?
Из теории вероятностей известно, что с вероятностью 0,67 значения случайной величины x, распределённой по нормальному закону, лежат в пределах:

и с вероятностью 0,997
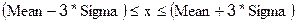 .
.
Для рассмотренного выше примера это означает, что для 67 % усилителей их усиление лежит в пределах
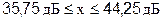
и для 99,7 % усилителей их усиление лежит в пределах
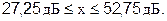
Таким образом, величины Mean и Sigma дают возможность предсказать, какое количество усилителей будет удовлетворять требованиям ТУ. То же самое можно определить по гистограмме, но при малом числе выборок точность результатов с применением Mean и Sigma выше. Для получения требуемой достоверности результата по гистограмме необходимо было бы провести не 25, а 1000 испытаний.
Дата добавления: 2016-11-29; просмотров: 1235;











