Понятие о спектральном анализе

Как известно из курса математики, сигнал U(t) на входе или выходе РЭС, заданный на отрезе времени [0,T], может быть разложен в ряд Фурье по базисным функциям, в качестве которых чаще всего рассматриваются тригонометрические функции. Таким образом, справедливо следующее представление сигнала:

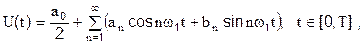
где 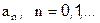- коэффициенты ряда Фурье,

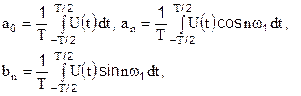
w₁=2pf₁=2p/T – круговая частота первой гармоники,

w_n=2pf_n=n2p/T – круговая частота n-ой гармоники, кратная частоте первой гармоники.

Знак равенства в представленном выражении означает, что стоящий в правой части ряд Фурье сходится к сигналу U(t) для 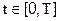. Это справедливо в том случае, если сигнал U(t) удовлетворяет условиям Дирихле. Оставив в стороне обсуждение этих условий, будем считать, что для реальных сигналов эти условия выполняются.

Введём замену переменных:

a_n = A_n cos j_n , b_n= A_n sin j_n , где

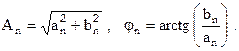
Тогда сигнал U(t) будет записан в виде:

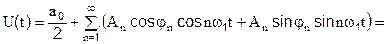
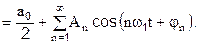
Здесь величины a₀, A_n, n = 1,2, …составляют амплитудный спектр сигнала, а величины j_n, n = 1,2, … составляют фазовый спектр.

Такими же спектрами обладает периодический сигнал S(t+nT) = S(t), заданный на всей оси времени [0,∞).

Оба спектра сигнала являются дискретными и иногда называются линейчатыми, в связи с изображением его в виде линий на графиках, пример которых условно показан на рис. 3.1.

Зачем нужно спектральное представление сигнала? Знание спектра сигнала позволяет определить диапазон частот, занимаемый сигналом, и, следовательно, необходимую ширину канала, который используется при записи сигнала на различные носители, либо при передаче сигнала по каналу связи.

Такое представление о спектре утвердилось в 30-х годах 20 века после разрешения парадокса сигнала с амплитудной модуляцией (АМ). В некоторых научных публикациях доказывалось, что АМ сигнал представляет собой синусоидальный сигнал, амплитуда которого меняется во времени. Следовательно, по мнению авторов, такой сигнал имеет лишь одну спектральную линию, а представление о спектре сигнала, определяемого рядом Фурье, является математической абстракцией и не имеет ничего общего с реальным сигналом. Естественно, что практика разработки и эксплуатации РЭС быстро разрешила этот парадокс.

Второй областью применения спектрального представления сигнала является традиционная оценка степени нелинейных искажений сигнала. При прохождении сигнала через нелинейное устройство его спектр обогащается дополнительными спектральными составляющими. Отношение мощности дополнительных спектральных составляющих к мощности исходного спектра определяет коэффициент нелинейных искажений.

Наконец, широко используемые принципы и методы сжатия аудио и видеосигнала основаны на вычислении спектра сигнала с последующим его преобразованием.

Существующие системы компьютерного моделирования имеют подпрограммы анализа Фурье, обеспечивающие вычисление спектра сигнала на основе дискретных преобразований Фурье.